题目内容
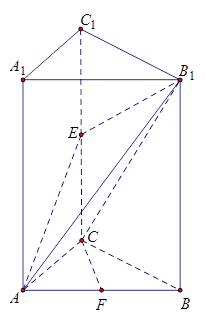
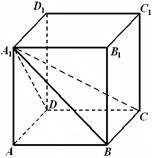
如图在长方体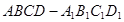 中,
中,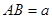 ,
,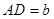 ,
,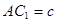 ,点
,点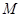 为
为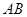 的中点,点
的中点,点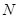 为
为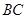 的中点.
的中点.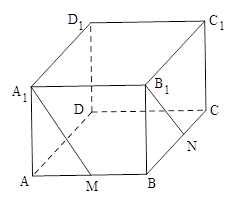
(1)求长方体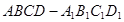 的体积;
的体积;
(2)若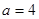 ,
,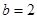 ,
,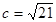 ,求异面直线
,求异面直线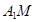 与
与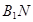 所成的角.
所成的角.
(1)  ;(2)
;(2) .
.
解析试题分析:(1)长方体的体积等于从同一顶点出发的三条棱长的乘积,这里只有两条棱长,另外一条线段是对角线,可根据对角线的计算公式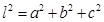 (
( 是三条棱长,
是三条棱长, 是对角线长)求得第三条棱长;(2)求异面直线所成的角,必须通过作平行线作出它们所成的角,而一般情况下,都是过其中一条直线上的一点作另一条的平行线,本题中只要取
是对角线长)求得第三条棱长;(2)求异面直线所成的角,必须通过作平行线作出它们所成的角,而一般情况下,都是过其中一条直线上的一点作另一条的平行线,本题中只要取 中点
中点 ,联接
,联接 ,可证
,可证 ∥
∥ ,从而
,从而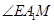 (或其补角)就是所示异面直线所成的角,在
(或其补角)就是所示异面直线所成的角,在 可解得.
可解得.
试题解析:(1) 连 、
、 .
.
 是直角三角形,
是直角三角形,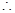
 . 1分
. 1分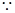
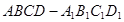 是长方体,
是长方体,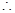
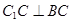 ,
, ,又
,又 ,
,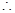
 平面
平面 ,
,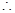
 .
.
又在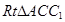 中,
中,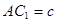 ,
, ,
,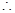
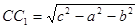 , 4分
, 4分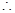
 6分
6分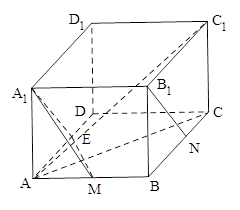
(2)取 的中点
的中点 ,连
,连 、
、 .
.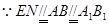 ,
,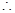 四边形
四边形 为平行四边形,
为平行四边形, ,
,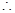
 等于异面直线
等于异面直线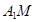 与
与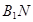 所成的角或其补角. 8分
所成的角或其补角. 8分
 ,
, ,
, ,得
,得 ,
, ,
, , 10分
, 10分
 ,
, .
.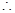 异面直线
异面直线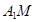 与
与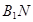 所成的角等于
所成的角等于 12分
12分
考点:(1)长方体的体积;(2)异面直线所成的角.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
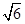 .
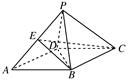
.
 是圆柱体
是圆柱体 的一条母线,
的一条母线, 过底面圆的圆心
过底面圆的圆心 ,
, 是圆
是圆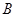 、
、 重合的任意一点,已知棱
重合的任意一点,已知棱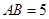 ,
,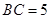 ,
,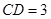 .
.
 ;
;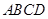 绕母线
绕母线 的三边在旋转过程中所围成的几何体的体积.
的三边在旋转过程中所围成的几何体的体积. 平面
平面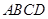 ,四边形
,四边形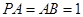 ,
,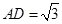 ,点
,点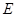 ,
,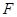 分别是
分别是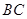 ,
,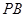 的中点.
的中点.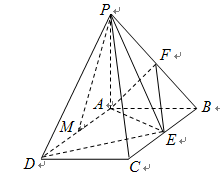
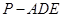 的体积;
的体积; 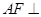 平面
平面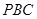 ;
; 为线段
为线段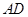 中点,求证:
中点,求证: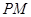 ∥平面
∥平面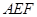 .
.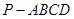 中,底面
中,底面 是边长为1的正方形,
是边长为1的正方形,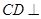 平面
平面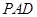 ,
, 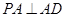 ,
,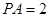 ,
,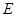 为
为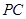 的中点,
的中点,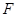 在棱
在棱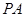 上.
上.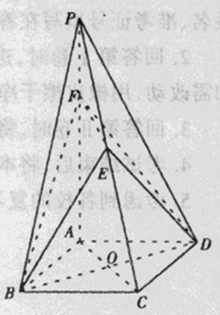
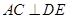 ;
;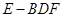 的体积.
的体积. 的棱长为
的棱长为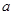 .
.
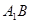 与
与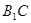 所成角的大小;
所成角的大小;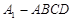 的体积.
的体积. 的中点,F在棱CC1上。
的中点,F在棱CC1上。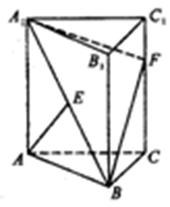
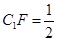 CF时,求多面体ABCFA1的体积;
CF时,求多面体ABCFA1的体积;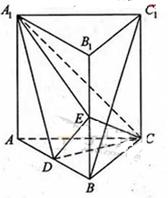
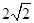 ,求三棱锥C一A1DE的体积.
,求三棱锥C一A1DE的体积.