题目内容
已知M是抛物线y2=-8x上的一个动点,M到直线x=2的距离是d1,M到直线x-y=4的距离是d2,则d1+d2的最小值是( )
| A、0 | ||
B、2
| ||
C、3
| ||
| D、不存在 |
分析:由题意得抛物线的焦点为F(-2,0)、准线为x=2.根据抛物线的定义可得d1+d2=|MF|+d2,再利用平面几何的知识可得当MF所在直线与直线x-y=4垂直时,点F到直线x-y=4的距离就是d1+d2的最小值,利用点到直线的距离公式加以计算,可得答案.
解答:解:∵抛物线y2=-8x中,2p=8,可得
=2,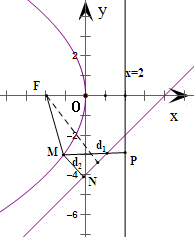
∴抛物线的焦点为F(-2,0),准线为x=2.
根据抛物线的定义,M到直线x=2的距离是d1=|MF|,
设点F到直线x-y=4的距离是d,
则由平面几何的知识可得:d1+d2=|MF|+d2≥d,
当且仅当MF所在直线与直线x-y=4垂直时,
d1+d2有最小值,最小值为d=
=3
.
故选:C
| p |
| 2 |

∴抛物线的焦点为F(-2,0),准线为x=2.
根据抛物线的定义,M到直线x=2的距离是d1=|MF|,
设点F到直线x-y=4的距离是d,
则由平面几何的知识可得:d1+d2=|MF|+d2≥d,
当且仅当MF所在直线与直线x-y=4垂直时,
d1+d2有最小值,最小值为d=
| |-2-0-4| | ||
|
| 2 |
故选:C
点评:本题给出抛物线的准线与另一条定直线,求抛物线上动点到两条直线的距离之和的最小值.着重考查了点到直线的距离公式、抛物线定义与标准方程等知识,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知M是抛物线y2=2px(p>0)上的点,若M到此抛物线的准线和对称轴的距离分别为5和4,则点M的横坐标为( )
| A、1 | B、1或4 | C、1或5 | D、4或5 |