题目内容
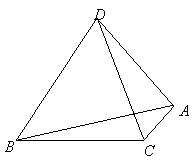
如图,![]() 为空间四点.在
为空间四点.在![]() 中,
中,![]() .等边三角形
.等边三角形![]() 以
以![]() 为轴运动.
为轴运动.
(Ⅰ)当平面![]() 平面
平面![]() 时,求
时,求![]() ;
;
(Ⅱ)当![]() 转动时,是否总有
转动时,是否总有![]() ?证明你的结论.
?证明你的结论.
解:(Ⅰ)取![]() 的中点
的中点![]() ,连结
,连结![]() ,
,
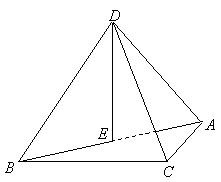
因为![]() 是等边三角形,所以
是等边三角形,所以![]() .
.
当平面![]() 平面
平面![]() 时,
时,
因为平面![]() 平面
平面![]()
![]() ,
,
所以![]() 平
平![]() 面
面![]() ,
,
可知![]()
![]()
由已知可得![]()
![]() ,
,
在![]() 中,
中,![]() .
.
(Ⅱ)当![]() 以
以![]() 为轴转动时,总有
为轴转动时,总有![]() .
.
证明:
(ⅰ)当![]() 在平面
在平面![]() 内时,因为
内时,因为![]() ,
,
所以![]() 都在线段
都在线段![]() 的垂直平分线上,即
的垂直平分线上,即![]() .
.
(ⅱ)当![]() 不在平面
不在平面![]() 内时,由(Ⅰ)知
内时,由(Ⅰ)知![]() .
.
又因![]() ,所以
,所以![]() .
.
又![]() 为相交直线,所以
为相交直线,所以![]() 平面
平面![]() ,
,
由![]() 平面
平面![]() ,得
,得![]() .
.
综上所述,总有![]()

练习册系列答案
相关题目

 为空间四点.在
为空间四点.在 中,
中, 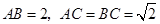 .等边三角形
.等边三角形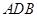 以
以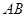 为轴运动.
为轴运动.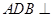 平面
平面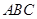 时,求
时,求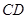 ;
; 转动时,证明总有
转动时,证明总有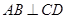 ?
?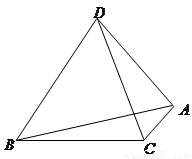
 为空间四点.在
为空间四点.在 中,
中, .等
.等 以
以 为轴运动.
为轴运动. 平面
平面 时,求
时,求 ;
; 转动时,是否总有
转动时,是否总有 ?证明你的结论.
?证明你的结论.
 为空间四点.在
为空间四点.在 中,
中, .等边三角形
.等边三角形 以
以 为轴运动.
为轴运动. 平面
平面 时,求
时,求 ;
; 转动时,是否总有
转动时,是否总有 ?证明你的结论.
?证明你的结论.
 如图,
如图, 为空间四点.在
为空间四点.在 中,
中, .等边三角形
.等边三角形 以
以 为轴运动.
为轴运动. 平面
平面 时,求
时,求 ;
; 转动时,是否总有
转动时,是否总有 ?证明你的结论.
?证明你的结论.