题目内容
(本小题满分12分)如图,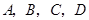 为空间四点.在
为空间四点.在 中,
中, 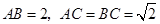 .等边三角形
.等边三角形 以
以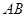 为轴运动.
为轴运动.
(1)当平面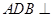 平面
平面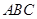 时,求
时,求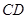 ;
;
(2)当 转动时,证明总有
转动时,证明总有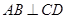 ?
?
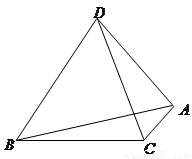
【答案】
(1) . (2)证明:见解析。
. (2)证明:见解析。
【解析】本题考查用线面垂直的方法来证明线线垂直,考查答题者的空间想象能力.
(Ⅰ)取出AB中点E,连接DE,CE,由等边三角形ADB可得出DE⊥AB,又平面ADB⊥平面ABC,故DE⊥平面ABC,在Rt△DEC中用勾股定理求出CD.
(Ⅱ)总有AB⊥CD,当D∈面ABC内时,显然有AB⊥CD,当D在而ABC外时,可证得AB⊥平面CDE,定有AB⊥CD.
解:(1)取 的中点
的中点 ,连结
,连结 ,因为
,因为 是等边三角形,所以
是等边三角形,所以 .
.
当平面 平面
平面 时,因为平面
时,因为平面 平面
平面
 ,
,
所以 平面
平面 ,可知
,可知
 …………4分
…………4分
由已知可得 ,
,
在 中,
中, .
…………6分
.
…………6分
(2)证明:
(ⅰ)当 在平面
在平面 内时,因为
内时,因为 ,
,
所以 都在线段
都在线段 的垂直平分线上,即
的垂直平分线上,即 .
.
(ⅱ)当 不在平面
不在平面 内时,由(Ⅰ)知
内时,由(Ⅰ)知 .
.
又因 ,所以
,所以 .
.
又 为相交直线,所以
为相交直线,所以 平面
平面 ,
,
由 平面
平面 ,得
,得 .
.
综上所述,总有 .
…………12分
.
…………12分

练习册系列答案
相关题目