题目内容
已知f(x)=x(x-a)(x-b),点A(s,f(s)),B(t,f(t)).
(Ⅰ)若a=b=1,求函数f(x)的单调递增区间;
(Ⅱ)若函数f(x)的导函数![]() 满足:当|x|≤1时,有
满足:当|x|≤1时,有![]()
![]() 恒成立,求函数f(x)的解析表达式;
恒成立,求函数f(x)的解析表达式;
(Ⅲ)若0<a<b,函数f(x)在x=s和x=t处取得极值,且![]() ,证明:
,证明:![]() 与
与![]() 不可能垂直.
不可能垂直.
答案:
解析:
解析:
|
解:(Ⅰ) 令 故 (Ⅱ) 当x∈[-1,1]时,恒有| 故有 及 即 ①+②,得 又由③,得 故 (Ⅲ)假设 即 故(s-a)(s-b)(t-a)(t-b)=-1 [st-(s+t)a+a2][st-(s+t)b+b2]=-1,………………………11分 由s,t为 从而有ab(a-b)2=9.………………………12分 这样 即 故 |

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
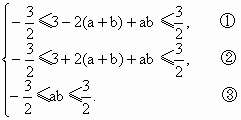 ………………………6分
………………………6分
