��Ŀ����
��ƽ��ֱ������ϵxOy��,F��������C:x2=2py(p>0)�Ľ���,M��������C��λ�ڵ�һ�����ڵ�����һ��,��M,F,O�����Բ��Բ��ΪQ,��Q��������C���ߵľ���Ϊ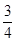 .
.
(1)��������C�ķ���;
(2)�Ƿ���ڵ�M,ʹ��ֱ��MQ��������C�����ڵ�M?������,�����M������;��������,˵������.
(3)����M�ĺ�����Ϊ ,ֱ��l:y=kx+
,ֱ��l:y=kx+ ��������C��������ͬ�Ľ���A,B,l��ԲQ��������ͬ�Ľ���D,E,��
��������C��������ͬ�Ľ���A,B,l��ԲQ��������ͬ�Ľ���D,E,�� ��k��2ʱ,|AB|2+|DE|2����Сֵ.
��k��2ʱ,|AB|2+|DE|2����Сֵ.
��1��x2=2y ��2�����ڵ�M( ,1) ��3��
,1) ��3��
������:(1)������֪F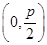 ,Բ��Q���߶�OF�Ĵ�ֱƽ����y=
,Բ��Q���߶�OF�Ĵ�ֱƽ����y= ��,
��,
��Ϊ������C���߷���Ϊy=-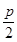 ,
,
����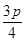 =
=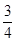 ,
,
��p=1.
���������C�ķ���Ϊx2=2y.
(2)������ڵ�M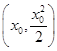 (x0>0)��������,������C�ڵ�M��������б��Ϊy��
(x0>0)��������,������C�ڵ�M��������б��Ϊy��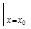 =
=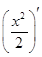
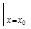 =x0,
=x0,
����ֱ��MQ�ķ���Ϊy-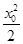 =x0(x-x0).
=x0(x-x0).
��y= ��xQ=
��xQ= +
+ .
.
����Q�� +
+ ,
, ��.
��.
��|QM|=|OQ|,
�ʣ� -
- ��2+��
��2+�� -
-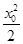 ��2=��
��2=�� +
+ ��2+
��2+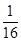 ,
,
��ˣ� -
-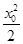 ��2=
��2=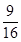 .
.
��x0>0,
����x0= ,��ʱM(
,��ʱM( ,1).
,1).
�ʴ��ڵ�M( ,1),
,1),
ʹ��ֱ��MQ��������C�����ڵ�M.
(3)��x0= ʱ,��(2)��Q��
ʱ,��(2)��Q��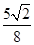 ,
, ��,
��,
��Q�İ뾶Ϊr=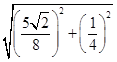 =
= ,
,
���Ԩ�Q�ķ���Ϊ��x-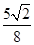 ��2+��y-
��2+��y- ��2=
��2=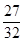 .
.
��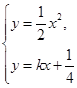
������2x2-4kx-1=0.
��A,B���������ֱ�Ϊ(x1,y1),(x2,y2),
���ڦ�1=16k2+8>0,x1+x2=2k,x1x2=- ,
,
����|AB|2=(1+k2)[(x1+x2)2-4x1x2]
=(1+k2)(4k2+2).
��
������(1+k2)x2-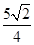 x-
x-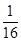 =0.
=0.
��D,E���������ֱ�Ϊ(x3,y3),(x4,y4),
���ڦ�2=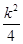 +
+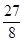 >0,x3+x4=
>0,x3+x4=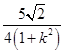 ,
,
x3x4=- .
.
����|DE|2=(1+k2)[(x3+x4)2-4x3x4]
= +
+ .
.
���|AB|2+|DE|2=(1+k2)(4k2+2)+  +
+ .
.
��1+k2=t,
���� ��k��2,
��k��2,
�� ��t��5,
��t��5,
����|AB|2+|DE|2=t(4t-2)+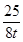 +
+
=4t2-2t+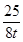 +
+
 ��У����ϵ�д�
��У����ϵ�д�
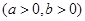 ����
����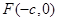
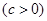 ������б��Ϊ
������б��Ϊ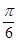 ��ֱ��
��ֱ�� ����˫������֧�ڵ�
����˫������֧�ڵ� ����
����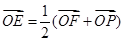 ����
����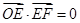 ����˫���ߵ�������Ϊ__________��
����˫���ߵ�������Ϊ__________�� ,����F1��x��Ĵ��߽���Բ��A��A������,
,����F1��x��Ĵ��߽���Բ��A��A������,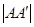 =4.
=4.

 -
- =1(a>0,b>0),������e=
=1(a>0,b>0),������e= ,���㵽�����ߵľ���Ϊ
,���㵽�����ߵľ���Ϊ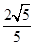 .
.
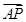 =��
=��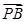 ,�ˡ�
,�ˡ�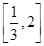 .���AOB�������ȡֵ��Χ.
.���AOB�������ȡֵ��Χ. +
+ =1(a>b>0)����,�ҽ���ֱ�ΪF1,F2,��P(a,b)����|PF2|=|F1F2|.
=1(a>b>0)����,�ҽ���ֱ�ΪF1,F2,��P(a,b)����|PF2|=|F1F2|. )2=16�ཻ��M,N����,��|MN|=
)2=16�ཻ��M,N����,��|MN|= |AB|,����Բ�ķ���.
|AB|,����Բ�ķ���. ����
����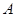 ��б��Ϊ2��ֱ�ߣ�����Բ����һ������Ϊ
��б��Ϊ2��ֱ�ߣ�����Բ����һ������Ϊ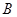 ����
����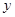 ��Ľ���Ϊ
��Ľ���Ϊ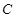 ����֪
����֪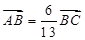 .
.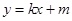 ����Բ����ֻ��һ��������
����Բ����ֻ��һ��������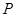 ������ֱ��
������ֱ��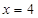 �ཻ�ڵ�
�ཻ�ڵ�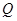 ����
����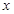 ���ϴ���һ����
���ϴ���һ���� ��ʹ��
��ʹ��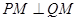 ������Բ�ķ���.
������Բ�ķ���.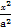 +
+ =1(a>b>0)���ҽ���ΪF(1,0),�ҵ�(-1,
=1(a>b>0)���ҽ���ΪF(1,0),�ҵ�(-1,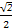 )����ԲC��.
)����ԲC��. ,0),��ֱ��l����F,��ֱ��l����ԲC����A,B����,֤��:
,0),��ֱ��l����F,��ֱ��l����ԲC����A,B����,֤��: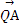 ��
��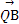 Ϊ��ֵ.
Ϊ��ֵ.