题目内容
已知焦点在x轴上,离心率为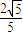 的椭圆的一个顶点是抛物线x2=4y的焦点,过椭圆右焦点F的直线l交椭圆于A、B两点,交y轴于点M,且
的椭圆的一个顶点是抛物线x2=4y的焦点,过椭圆右焦点F的直线l交椭圆于A、B两点,交y轴于点M,且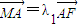 ,
,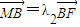 .
.(1)求椭圆的方程;
(2)证明:λ1+λ2为定值.
【答案】分析:(1)因为椭圆的离心率为 ,所以
,所以 ,又因为椭圆的一个顶点是抛物线x2=4y的焦点,且椭圆的焦点在x轴上,所以b=1,再根据a,b,c的关系,就能求出a的值,椭圆的方程可得.
,又因为椭圆的一个顶点是抛物线x2=4y的焦点,且椭圆的焦点在x轴上,所以b=1,再根据a,b,c的关系,就能求出a的值,椭圆的方程可得.
(2)可先设出A、B、M的坐标,代入 ,
, ,就可找到几个点坐标的关系式,再根据A,B再椭圆上,满足椭圆方程,消去参数,就可求出λ1+λ2的值.
,就可找到几个点坐标的关系式,再根据A,B再椭圆上,满足椭圆方程,消去参数,就可求出λ1+λ2的值.
解答:解:(1)依题意,设椭圆方程为
因为抛物线x2=4y的焦点为(0,1),所以b=1.
由 .
.
故椭圆方程为 .
.
(2)依题意设分别为(x1,y1),(x2,y2),(0,y),
由(1)得椭圆的右焦点F(2,0),

由
由
因为A、B在椭圆上,所以
即
所以λ1,λ2是方程λ2+10λ+(5-5y2)=0的两根,
故λ1+λ2=-10是定值.
点评:本题考查了直线与椭圆 的位置关系,做题时要认真分析,找到突破口.
 ,所以
,所以 ,又因为椭圆的一个顶点是抛物线x2=4y的焦点,且椭圆的焦点在x轴上,所以b=1,再根据a,b,c的关系,就能求出a的值,椭圆的方程可得.
,又因为椭圆的一个顶点是抛物线x2=4y的焦点,且椭圆的焦点在x轴上,所以b=1,再根据a,b,c的关系,就能求出a的值,椭圆的方程可得.(2)可先设出A、B、M的坐标,代入
 ,
, ,就可找到几个点坐标的关系式,再根据A,B再椭圆上,满足椭圆方程,消去参数,就可求出λ1+λ2的值.
,就可找到几个点坐标的关系式,再根据A,B再椭圆上,满足椭圆方程,消去参数,就可求出λ1+λ2的值.解答:解:(1)依题意,设椭圆方程为

因为抛物线x2=4y的焦点为(0,1),所以b=1.
由
 .
.故椭圆方程为
 .
.(2)依题意设分别为(x1,y1),(x2,y2),(0,y),
由(1)得椭圆的右焦点F(2,0),

由

由

因为A、B在椭圆上,所以

即

所以λ1,λ2是方程λ2+10λ+(5-5y2)=0的两根,
故λ1+λ2=-10是定值.
点评:本题考查了直线与椭圆 的位置关系,做题时要认真分析,找到突破口.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
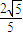 的椭圆的一个顶点是抛物线x2=4y的焦点,过椭圆右焦点F的直线l交椭圆于A、B两点,交y轴于点M,且
的椭圆的一个顶点是抛物线x2=4y的焦点,过椭圆右焦点F的直线l交椭圆于A、B两点,交y轴于点M,且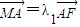 ,
,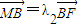 .
.