题目内容
数列{xn}满足：x1=1，x2=-1，且xn-1+xn+1=2xn（n≥2），则xn=________．
-2n+3
分析：根据所给的递推式，看出数列符合等差数列的定义，得到数列是一个等差数列，根据所给的两项做出数列的公差，写出通项公式．
解答：∵xn-1+xn+1=2xn（n≥2），
∴数列是一个等差数列，
∵x1=1，x2=-1，
∴d=-1-1=-2
∴xn=x1+（-2）（n-1）=-2n+3
故答案为：-2n+3
点评：本题考查数列的通项公式，本题解题的关键是判断数列是一个等差数列，再进一步应用等差数列的性质，本题是一个基础题．
分析：根据所给的递推式，看出数列符合等差数列的定义，得到数列是一个等差数列，根据所给的两项做出数列的公差，写出通项公式．
解答：∵xn-1+xn+1=2xn（n≥2），
∴数列是一个等差数列，
∵x1=1，x2=-1，
∴d=-1-1=-2
∴xn=x1+（-2）（n-1）=-2n+3
故答案为：-2n+3
点评：本题考查数列的通项公式，本题解题的关键是判断数列是一个等差数列，再进一步应用等差数列的性质，本题是一个基础题．
练习册系列答案
相关题目
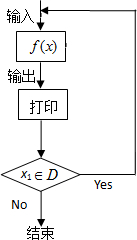对任何函数f（x），x∈D，可按图示构造一个数列发生器，其工作原理如下：①输入数据x0∈D，经数列发生器输出x1=f（x0）；②若x1∉D，则数列发生器结束工作；若x1∈D，则将x1反馈回输入端，再输出x2=f（x1），并依此规律继续下去．现定义
请认真阅读下列程序框图：