题目内容
在线性条件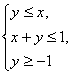
下，求z=2x-y的最大值和最小值.
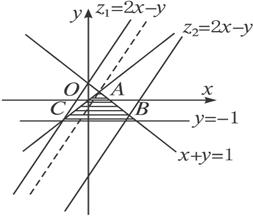
解：约束条件的可行域如右图中△ABC的内部加上边界.
当z为常数时,-z表示直线z=2x-y在y轴上的截距.
如图所示,当点(x,y)位于C(-1,-1)时,-z取最大值.
∴z有最小值,zmin=2×(-1)-(-1)=-1.
当点(x,y)位于B(2,-1)时,-z取最小值,
∴z有最大值,zmax=2×2-(-1)=5.
新思维寒假作业系列答案（本小题满分12分）
班主任为了对本班学生的考试成绩进行分析，决定从全班25位女同学，15位男同学中随机抽取一个容量为8的样本进行分析．
（1）如果按性别比例分层抽样，则样本中男、女生各有多少人；
（2）随机抽取8位同学，数学分数依次为：60，65，70，75，80，85，90，95；
物理成绩依次为：72，77，80，84，88，90，93，95，
①若规定80分（含80分）以上为良好，90分（含90分）以上为优秀，在良好的条件下，求两科均为优秀的概率；
②若这8位同学的数学、物理分数事实上对应下表：
| 学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 数学分数 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95[来源:Z&xx&k.Com] |
| 物理分数 | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
根据上表数据可知，变量
与
之间具有较强的线性相关关系，求出与的线性回归方程（系数精确到0.01）．（参考公式：
，其中
，
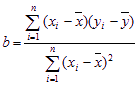；参考数据：
，
，
，
，
，
，
）
（本小题满分12分）
班主任为了对本班学生的考试成绩进行分析，决定从全班25位女同学，15位男同学中随机抽取一个容量为8的样本进行分析．
（1）如果按性别比例分层抽样，则样本中男、女生各有多少人；
（2）随机抽取8位同学，数学分数依次为：60，65，70，75，80，85，90，95；
物理成绩依次为：72，77，80，84，88，90，93，95，
①若规定80分（含80分）以上为良好，90分（含90分）以上为优秀，在良好的条件下，求两科均为优秀的概率；
②若这8位同学的数学、物理分数事实上对应下表：
|
学生编号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
数学分数 |
60 |
65 |
70 |
75 |
80 |
85 |
90 |
95[来源:Z&xx&k.Com] |
|
物理分数 |
72 |
77 |
80 |
84 |
88 |
90 |
93 |
95 |
根据上表数据可知，变量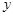
与
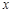之间具有较强的线性相关关系，求出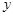与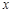的线性回归方程（系数精确到0.01）．（参考公式：
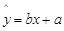，其中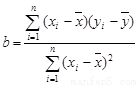
，
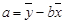；参考数据：
，
，
，
，
，
，
）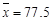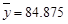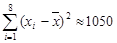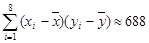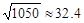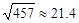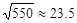