Question

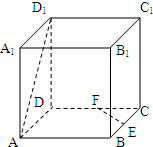如图，在正方体ABCD-A₁B₁C₁D₁中，AA₁=a，E，F分别是BC，DC的中点．
（1）求直线BD₁与平面ABCD所成角的正切值；
（2）求异面直线AD₁与EF所成角的大小．

Answer 1

分析：（1）确定∠D₁BD是直线BD₁与平面ABCD所成角，在直角△D₁DB中，可得结论；
（2）连结BC₁、BD和DC₁，证明∠DBC₁就是异面直线AD₁与EF所成角，即可得出结论．

解答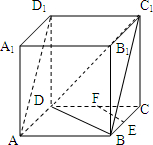：解：（1）在正方体ABCD-A₁B₁C₁D₁中，BD是BD₁在平面ABCD内的射影，
所以∠D₁BD是直线BD₁与平面ABCD所成角．
设正方体的棱长为a，在直角△D₁DB中，D₁D=a，BD=

2

a，∠D₁DB=90°，
则tan∠D₁DB=

DD1

BD

=

2

2

；                            6分
（2）连结BC₁、BD和DC₁，在正方体ABCD-A₁B₁C₁D₁中，
由AB∥D₁C₁且AB=D₁C₁有ABC₁D₁是平行四边形，
∴AD₁∥BC₁
在△BCD中，E，F分别是BC，DC的中点，
∴有EF∥BD，所以∠DBC₁就是异面直线AD₁与EF所成角
在正方体ABCD-A₁B₁C₁D₁中，BC₁、BD和DC₁是其三个面上的对角线，它们相等．
所以△DBC₁是正三角形，∠DBC₁=60°
故异面直线AD₁与EF所成角的大小为60°                         13分

点评：本题考查线面角，考查线线角，考查学生的计算能力，正确作出空间角是关键．