题目内容
已知函数 ,数列{an}满足a1=1,an+1=f(an)(n∈N+).
,数列{an}满足a1=1,an+1=f(an)(n∈N+).
(1)求数列{an}的通项公式an;
(2)若数列{bn}满足 ,求Sn.
,求Sn.
解:(1)由已知,an+1= ,所以
,所以 =
= +1,
+1,
∴ +
+ =3(
=3( +
+ ),
),
∴数列{ }是以1+
}是以1+ =
= 为首项,以3为公比的等比数列.
为首项,以3为公比的等比数列.
∴ =
= •3 n-1=
•3 n-1=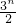 ,
, =
=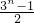
所以an=
(2) =
= =
= -
-
Sn=b1+b2+…+bn= -
- +(
+( -
- )+…+(
)+…+( -
- )=
)= -
-
分析:(1)由已知,an+1= ,构造出
,构造出 +
+ =3(
=3( +
+ )求出数列{
)求出数列{ }的通项后再求数列{an}的通项公式an;
}的通项后再求数列{an}的通项公式an;
(2)由(1)可求得 =
= =
= -
- ,经这样裂项后再求和.
,经这样裂项后再求和.
点评:本题主要考查由递推公式推导数列的通项公式,考查等比数列的判定、通项公式求解,裂项求和法,考查变形构造、转化、计算能力.
 ,所以
,所以 =
= +1,
+1,∴
 +
+ =3(
=3( +
+ ),
),∴数列{
 }是以1+
}是以1+ =
= 为首项,以3为公比的等比数列.
为首项,以3为公比的等比数列.∴
 =
= •3 n-1=
•3 n-1=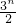 ,
, =
=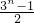
所以an=

(2)
 =
= =
= -
-
Sn=b1+b2+…+bn=
 -
- +(
+( -
- )+…+(
)+…+( -
- )=
)= -
-
分析:(1)由已知,an+1=
 ,构造出
,构造出 +
+ =3(
=3( +
+ )求出数列{
)求出数列{ }的通项后再求数列{an}的通项公式an;
}的通项后再求数列{an}的通项公式an;(2)由(1)可求得
 =
= =
= -
- ,经这样裂项后再求和.
,经这样裂项后再求和.点评:本题主要考查由递推公式推导数列的通项公式,考查等比数列的判定、通项公式求解,裂项求和法,考查变形构造、转化、计算能力.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
 ,数列an满足
,数列an满足 .
.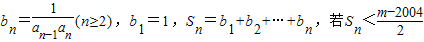 对一切n∈N*成立,求最小正整数m.
对一切n∈N*成立,求最小正整数m.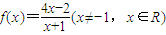 ,数列{an}满足 a1=a(a≠-1,a∈R),an+1=f(an)(n∈N*).
,数列{an}满足 a1=a(a≠-1,a∈R),an+1=f(an)(n∈N*). ,证明数列{bn}是等比数列,并求出通项公式an.
,证明数列{bn}是等比数列,并求出通项公式an. 若数列{an}满足an=
若数列{an}满足an= (n∈N+)且{an}是递减数列,则实数a的取值范围是( )
(n∈N+)且{an}是递减数列,则实数a的取值范围是( ) ,1) B.(
,1) B.(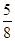 ) C.(
) C.( ) D.(
) D.( ,数列an满足an=f(n)(n∈N*),且an是递增数列,则实数a的取值范围是
,数列an满足an=f(n)(n∈N*),且an是递增数列,则实数a的取值范围是