题目内容
(1)设一次函数f(x)满足f(3)=2,f(2)=3,求f(5)的值;
(2)若函数f(x)的定义域为[a,b],值域为[a,b](a<b),则称函数f(x)是[a,b]上的“方正”函数.
①设g(x)=
x2-x+
是[a,b]上的“方正”函数,求常数a,b的值.
②问是否存在常数a,b(a>-2),使函数h(x)=
是区间[a,b]上的“方正”函数?若存在,求出a,b的值;不存在,说明理由.
(2)若函数f(x)的定义域为[a,b],值域为[a,b](a<b),则称函数f(x)是[a,b]上的“方正”函数.
①设g(x)=
| 1 |
| 2 |
| 3 |
| 2 |
②问是否存在常数a,b(a>-2),使函数h(x)=
| 1 |
| x+2 |
(1)设f(x)=mx+n(m≠0),又f(3)=2,f(2)=3,
所以3m+n=2,2m+n=3?m=-1,n=5
即f(x)=-x+5?f(5)=0;…(4分)
(2)①由g(x)=
(x-1)2+1≥1知g(x)在[a,b]上单调增函数且a≥1,
所以值域为[g(a),g(b)],
由已知g(x)=
x2-x+
是[1,b]上的“方正”函数,所以[g(a),g(b)]=[a,b]
则g(a)=a,g(b)=b,即a,b是方程g(x)=x的两个根(1≤a<b)
解方程
x2-x+
=x得x=1或x=3,所以a=1,b=3…(9分)
②假设存在常数a,b,使函数h(x)=
是区间[a,b]上的“方正”函数.
因a>-2,显然h(x)=
在区间[a,b]上是单调减函数,值域为[h(b),h(a)]=[a,b],
即
?
?
?(a+2)b=(b+2)a?a=b与a<b矛盾,
故不存在常数a,b,使函数h(x)=
是区间[a,b]上的“方正”函数.…(14分)
所以3m+n=2,2m+n=3?m=-1,n=5
即f(x)=-x+5?f(5)=0;…(4分)
(2)①由g(x)=
| 1 |
| 2 |
所以值域为[g(a),g(b)],
由已知g(x)=
| 1 |
| 2 |
| 3 |
| 2 |
则g(a)=a,g(b)=b,即a,b是方程g(x)=x的两个根(1≤a<b)
解方程
| 1 |
| 2 |
| 3 |
| 2 |
②假设存在常数a,b,使函数h(x)=
| 1 |
| x+2 |
因a>-2,显然h(x)=
| 1 |
| x+2 |
即
|
|
|
故不存在常数a,b,使函数h(x)=
| 1 |
| x+2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
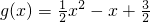 是[a,b]上的“方正”函数,求常数a,b的值.
是[a,b]上的“方正”函数,求常数a,b的值.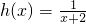 是区间[a,b]上的“方正”函数?若存在,求出a,b的值;不存在,说明理由.
是区间[a,b]上的“方正”函数?若存在,求出a,b的值;不存在,说明理由.