题目内容
已知a、b、c为等比数列,b、m、a和b、n、c是两个等差数列,则| a |
| m |
| c |
| n |
分析:先根据等差中项的性质可知 m=
(a+b),n=
代入
+
中,进而利用等比数列的通项公式化简整理即可求得答案.
| 1 |
| 2 |
| b+c |
| 2 |
| a |
| m |
| c |
| n |
解答:解:∵m-b=a-m,n-b=c-n,
∴m=
(a+b),n=
∴
+
=
+
=
+
=2
故答案为2
∴m=
| 1 |
| 2 |
| b+c |
| 2 |
∴
| a |
| m |
| c |
| n |
=
| a | ||
|
| ||
| 2 |
=
| 2a |
| a+aq |
| 2aq2 |
| aq+aq 2 |
=2
故答案为2
点评:本题主要考查了等差数列和等比数列的性质.解题的关键是利用等差中项的性质和利用等比数列的通项公式解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
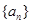 中,
中,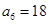 且
且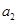 是
是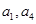 的等比中项,则它的第4项到第11项的和为
的等比中项,则它的第4项到第11项的和为