题目内容
13.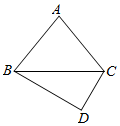 如图,在△ABC中,角A,B,C的对边分别为a,b,c,a=b(sinC+cosC).
如图,在△ABC中,角A,B,C的对边分别为a,b,c,a=b(sinC+cosC).(Ⅰ)求∠ABC;
(Ⅱ)若∠A=$\frac{π}{2}$,D为△ABC外一点,DB=2,DC=1,求四边形ABDC面积的最大值.
分析 (Ⅰ)利用正弦定理,三角函数恒等变换的应用化简已知可得cosBsinC=sinBsinC,结合sinC≠0,可求tanB=1,结合范围B∈(0,π),即可求得B的值.
(Ⅱ)由已知利用余弦定理可得BC2=12+22-2×1×2×cosD=5-4cosD,由已知及(Ⅰ)可知$∠ABC=\frac{π}{4}$,利用三角形面积公式可求S△ABC,S△BDC,从而可求${S_{四边形ABDC}}=\frac{5}{4}+\sqrt{2}sin(D-\frac{π}{4})$,根据正弦函数的性质即可得解四边形ABDC面积的最大值.
解答  (本题满分为12分)
(本题满分为12分)
解:(Ⅰ)在△ABC中,∵a=b(sinC+cosC),
∴sinA=sinB(sinC+cosC),…(1分)
∴sin(π-B-C)=sinB(sinC+cosC),
∴sin(B+C)=sinB(sinC+cosC),…(2分)
∴sinBcosC+cosBsinC=sinBsinC+sinBcosC,…(3分)
∴cosBsinC=sinBsinC,
又∵C∈(0,π),故sinC≠0,…(4分)
∴cosB=sinB,即tanB=1. …(5分)
又∵B∈(0,π),
∴$B=\frac{π}{4}$. …(6分)
(Ⅱ)在△BCD中,DB=2,DC=1,
∴BC2=12+22-2×1×2×cosD=5-4cosD. …(7分)
又$A=\frac{π}{2}$,由(Ⅰ)可知$∠ABC=\frac{π}{4}$,
∴△ABC为等腰直角三角形,…(8分)
∴${S_{△ABC}}=\frac{1}{2}×BC×\frac{1}{2}×BC=\frac{1}{4}B{C^2}=\frac{5}{4}-cosD$,…(9分)
又∵${S_{△BDC}}=\frac{1}{2}×BD×DC×sinD=sinD$,…(10分)
∴${S_{四边形ABDC}}=\frac{5}{4}-cosD+sinD=\frac{5}{4}+\sqrt{2}sin(D-\frac{π}{4})$. …(11分)
∴当$D=\frac{3π}{4}$时,四边形ABDC的面积有最大值,最大值为$\frac{5}{4}+\sqrt{2}$.…(12分)
点评 本题主要考查了正弦定理、余弦定理、三角形面积公式及三角恒等变换等基础知识的应用,考查了运算求解能力,考查了化归与转化思想、函数与方程思想,属于中档题.

 名校课堂系列答案
名校课堂系列答案(1)求函数y=Acos(ωt)+k(A>0)的解析式;
(2)浴场规定:当海浪高度高于1米时才对冲浪爱好者开放,根据以上数据,当天上午8:00时至晚上20:00时之间可供冲浪爱好者冲浪的时间约为多少时?
| t时 | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y米 | 1.5 | 1.0 | 0.5 | 0.98 | 1.5 | 1.01 | 0.5 | 0.99 | 1.5 |
| A. | (-2,0) | B. | (-2,1) | C. | (0,2) | D. | (0,1) |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分且必要条件 | D. | 既不充分也不必要条件 |