题目内容
已知函数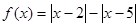 .
.
(I)证明: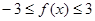 ;
;
(II)求不等式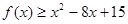 的解集.
的解集.
(Ⅰ)分类讨论去绝对值号进行证明即可(Ⅱ)
解析试题分析:(I)证明:当 时,
时, ;
;
当 时,
时, ,所以
,所以 ;
;
当 时,
时,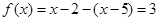 .
.
所以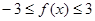 . ……5分
. ……5分
(II)由(I)可知,
当 时,
时, ,
,
∴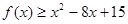 的解集为空集;
的解集为空集;
当 时,
时, ,
,
∴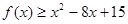 的解集为
的解集为 ;
;
当 时,
时, ,
,
∴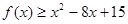 的解集为
的解集为 .
.
综上,不等式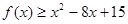 的解集为
的解集为 . ……10分
. ……10分
考点:本小题主要考查含绝对值的不等式的求解和二次不等式的解法.
点评:求解含绝对值的不等式的关键是通过分类讨论去掉绝对值号,分类讨论时要尽量做到不重不漏.

练习册系列答案
相关题目
 .
.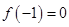 ,试判断函数
,试判断函数 零点个数;
零点个数; ,使
,使 同时满足以下条件
同时满足以下条件 ,且
,且 ;
; ,都有
,都有 。若存在,求出
。若存在,求出 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。 且
且 ,
, ,试证明存在
,试证明存在 ,
, 成立。
成立。 的最小值为1,且
的最小值为1,且 .
. 上不单调,求实数
上不单调,求实数 的取值范围;
的取值范围; 上,
上,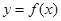 的图像恒在
的图像恒在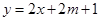 的图像上方,试确定实数
的图像上方,试确定实数 的取值范围.
的取值范围.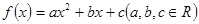 满足下列条件:①当
满足下列条件:①当 时,
时, 的最小值为
的最小值为 ,且图像关于直线
,且图像关于直线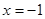 对称;②当
对称;②当 时,
时, 恒成立.
恒成立.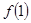 的值;
的值;  的解析式;
的解析式; 上恒有
上恒有 ,求实数
,求实数 的取值范围.
的取值范围.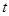 表示时间,以月为单位,年初为起点,根据历年数据,某水库的蓄水量(单位:亿立方米)关于
表示时间,以月为单位,年初为起点,根据历年数据,某水库的蓄水量(单位:亿立方米)关于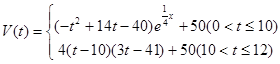
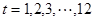 ),问:同一年内哪些月份是枯水期?
),问:同一年内哪些月份是枯水期?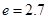 计算)
计算)
 个月的旅游人数的和
个月的旅游人数的和 (单位:万人)与
(单位:万人)与 已知第
已知第 (单位:元)与
(单位:元)与
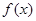 (单位:万人)与x的函数关系式;
(单位:万人)与x的函数关系式;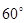 (如图),考虑到防洪堤坚固性及石块用料等因素,设计其断面面积为
(如图),考虑到防洪堤坚固性及石块用料等因素,设计其断面面积为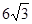 平方米,为了使堤的上面与两侧面的水泥用料最省,则断面的外周长(梯形的上底线段
平方米,为了使堤的上面与两侧面的水泥用料最省,则断面的外周长(梯形的上底线段 与两腰长的和)要最小.
与两腰长的和)要最小.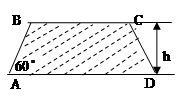
 的范围内,外周长最小为多少米?
的范围内,外周长最小为多少米? (0≤x≤5),点A、B分别是函数y=f(x)图像上的最高点和最低点.
(0≤x≤5),点A、B分别是函数y=f(x)图像上的最高点和最低点. ·
·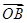 的值;
的值; 、
、 的终边上,求tan(
的终边上,求tan(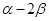 )的值.
)的值.