题目内容
【题目】已知A是圆锥的顶点,BD是圆锥底面的直径,C是底面圆周上一点,AC=BD=2,BC=1,点M在线段BD上,且BM![]() ,平面ABC和平面ACD将圆锥截去部分后的几何体如图所示.
,平面ABC和平面ACD将圆锥截去部分后的几何体如图所示.
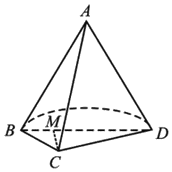
(1)求证:CM⊥AD;
(2)求AC与底面所成的角;
(3)求该几何体的体积.
【答案】(1)证明见解析(2)60°(3)![]()
【解析】
(1)在![]() 中通过解三角形得
中通过解三角形得![]() ,从而可证
,从而可证![]() 与平面
与平面![]() 垂直(取
垂直(取![]() 中点
中点![]() ,
,![]() 是圆锥的高),得线线垂直;
是圆锥的高),得线线垂直;
(2)由(1)![]() 是直线
是直线![]() 与底面所成的角,在三角形中求解即可;
与底面所成的角,在三角形中求解即可;
(3)该几何体是半个圆锥和一个三棱锥的组合体,由锥体体积公式计算.
(1)证明:∵C是底面圆周上一点,
∴BC⊥BD,
又∵![]() ,
,
∴∠BDC=30°,
∴∠CBD=60°,
在三角形BCM中,由余弦定理得:![]() ,
,
∴BC2=BM2+CM2,
∴CM⊥BD,
设O为BD的中点,连接AO,则AO⊥平面BCD,
∵CM在平面BCD内,
∴CM⊥AO,
又AO∩BD=O,
∴CM⊥平面BAD,
又AD在平面BAD内,
∴CM⊥AD;
(2)设O为BD的中点,连接CO,AO,则∠ACO为AC与底面所成的角,
由已知可得AB=AD=AC=BD=2,所以△ABD为正三角形,![]() ,
,
而CO=1,所以![]() ,
,
∴AC与底面所成的角为60°;
(3)由题设知,∠CBD=60°,
故△BCD的面积![]() ,
,
底面半圆的面积![]() ,
,
所以该几何体的体积![]() .
.
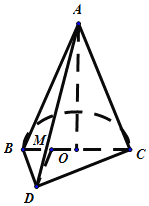

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目