题目内容
曲线y=
与直线y=x，x=2所围成的图形面积为
- A.
- B.2
- C.
+ln2 - D.-ln2
D
分析：曲线y=与直线y=x，x=2所围成的图形面积可用定积分计算，先求出图形横坐标范围，再求
即可．
解答：解联立
，得，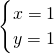
，
；∴曲线y=与直线y=x，x=2所围成的图形面积为
=（x2-lnx）|12=（
4-ln2）-（1-0）=-ln2
故选D
点评：本题考查了利用定积分求封闭图形的面积，做题时应认真分析．
分析：曲线y=
与直线y=x，x=2所围成的图形面积可用定积分计算，先求出图形横坐标范围，再求即可．解答：解联立
，得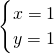，，；∴曲线y=
与直线y=x，x=2所围成的图形面积为=（x2-lnx）|12=（4-ln2）-（1-0）=-ln2故选D
点评：本题考查了利用定积分求封闭图形的面积，做题时应认真分析．
练习册系列答案
相关题目
与直线y=x,x=2所围成的图形的面积为 .
与直线y=x-1及x=4所围成的封闭图形的面积为（ ）
与直线y=x-1及x=4所围成的封闭图形的面积为（ ）
与直线y=x，x=2所围成的图形面积为（ ）
+ln2
-ln2
与直线y=x-1及x=4所围成的封闭图形的面积为（ ）