题目内容
已知等差数列![]() 满足:
满足:![]()
(1)是否存在常数![]() ,使得
,使得![]() 请对你的结论作出正确的解释或证明;
请对你的结论作出正确的解释或证明;
(2)当![]() 时,求数列
时,求数列![]() 的通项公式;
的通项公式;
(3)若![]() 是数列
是数列![]() 中的最小项,求首项
中的最小项,求首项![]() 的取值范围。
的取值范围。
(1)存在(2)![]() (3)
(3)![]()
解析:
(1)存在;
证明如下:因为![]()
![]() 与
与
![]() 比较,得
比较,得 解得
解得![]() ,
,
此时![]()
![]()
![]()
(2)由(1)知![]() 由于
由于![]() (否则,如
(否则,如![]() ,由递推式可以知道
,由递推式可以知道![]() ,进而可以知道
,进而可以知道![]() )故有
)故有![]() ,故
,故
数列 首项为
首项为![]() ,公差为1的等差数列,故
,公差为1的等差数列,故![]()
所以![]() 。
。
(3)由(2)知, ,易知函数
,易知函数![]() 在
在
![]() 时达到最小值,故有
时达到最小值,故有![]() ,
,
解答得![]()

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
 满足
满足 ,
, ,
, ,则
,则 的值为 .
的值为 . 满足:
满足: ,
, ,该数列的前三项分别加上
,该数列的前三项分别加上 ,
, 后顺次成为等比数列
后顺次成为等比数列 的前三项. 求数列
的前三项. 求数列 =____________
=____________ 满足,
满足,
 。(1)求
。(1)求 和
和
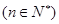 ,求数列
,求数列 的前n项和
的前n项和
 满足
满足 ,
, ,
,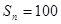 ,则
,则 的值为( )
的值为( ) B.
B. C.
C. D.
D.