题目内容
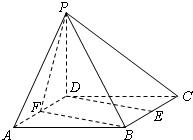 已知四棱锥P-ABCD的底面ABCD是边长为2的正方形,PD⊥底面ABCD,E,F分别为棱BC,AD的中点.
已知四棱锥P-ABCD的底面ABCD是边长为2的正方形,PD⊥底面ABCD,E,F分别为棱BC,AD的中点.
(Ⅰ)求证:DE∥平面PFB;
(Ⅱ)已知二面角P-BF-C的余弦值为 ,求四棱锥P-ABCD的体积.
,求四棱锥P-ABCD的体积.
 解:(Ⅰ)因为E,F分别为正方形ABCD的两边BC,AD的中点,
解:(Ⅰ)因为E,F分别为正方形ABCD的两边BC,AD的中点,所以
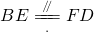 ,所以,BEDF为平行四边形,(2分)
,所以,BEDF为平行四边形,(2分)得ED∥FB,(3分)
又因为FB?平面PFB,且ED?平面PFB,(4分)
所以DE∥平面PFB.(5分)
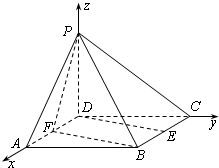
(Ⅱ)如图,以D为原点,射线DA,DC,DP分
别为x,y,z轴建立空间直角坐标系.设PD=a,
可得如下点的坐标:
P(0,0,a),F(1,0,0),B(2,2,0)
则有:
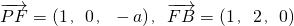 ,(6分)
,(6分)因为PD⊥底面ABCD,所以平面ABCD的
一个法向量为
 =(0,0,1),(.7分)
=(0,0,1),(.7分)设平面PFB的一个法向量为
 =(x,y,z),
=(x,y,z),则可得
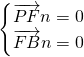 即
即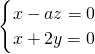
令x=1,得
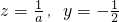 ,所以
,所以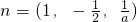 .(9分)
.(9分)由已知,二面角P-BF-C的余弦值为
 ,
,所以得:
 ,(10分)
,(10分)解得a=2.(11分)
因为PD是四棱锥P-ABCD的高,
所以,其体积为
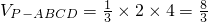 .(13分)
.(13分)分析:(Ⅰ)要证DE∥平面PFB,只需证明DE平行平面PFB内的直线FB,说明DE不在平面PFB内,即可.
(Ⅱ)以D为原点,射线DA,DC,DP分别为x,y,z轴建立空间直角坐标系.设PD=a,求出平面ABCD的一个法向量为
 ,平面PFB的一个法向量为
,平面PFB的一个法向量为 =(x,y,z),利用
=(x,y,z),利用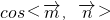 ,以及已知二面角P-BF-C的余弦值为
,以及已知二面角P-BF-C的余弦值为 ,求出a,然后求四棱锥P-ABCD的体积.
,求出a,然后求四棱锥P-ABCD的体积.点评:本题考查直线与平面平行的判定,棱柱、棱锥、棱台的体积,二面角及其度量,考查计算能力,逻辑思维能力,空间想象能力,是中档题.

练习册系列答案
相关题目
 如图,已知四棱锥P--ABC的底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,e为PC的中点,F为AD的中点.
如图,已知四棱锥P--ABC的底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,e为PC的中点,F为AD的中点. 如图,已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=2CD=2,PB=PC,侧面PBC⊥底面ABCD,O是BC的中点.
如图,已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=2CD=2,PB=PC,侧面PBC⊥底面ABCD,O是BC的中点. 已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,E为BC中点,AE与BD交于O点,AB=BC=2CD=2,BD⊥PE.
已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,E为BC中点,AE与BD交于O点,AB=BC=2CD=2,BD⊥PE. 如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,∠DAB=∠ABC=90°,E是线段PC上一点,PC⊥平面BDE.
如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,∠DAB=∠ABC=90°,E是线段PC上一点,PC⊥平面BDE.