题目内容
函数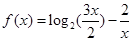 的零点一定位于区间( )
的零点一定位于区间( )
A.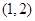 | B.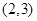 | C.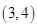 | D.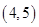 |
C
解析试题分析:根据题意,由于函数 的交点的位置就是零点所在的区域,那么可以利用零点存在性定理判定,由于
的交点的位置就是零点所在的区域,那么可以利用零点存在性定理判定,由于 ,故可知函数零点一定在区间
,故可知函数零点一定在区间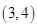 内,故答案为C.
内,故答案为C.
考点:函数的零点
点评:主要是考查了函数零点的求解,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
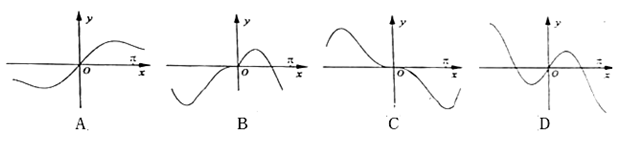
下列函数的图像一定关于原点对称的是( )
A. | B. | C. | D. |
已知函数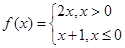 ,若f(a)+f(1)=0,则实数a的值等于( )
,若f(a)+f(1)=0,则实数a的值等于( )
| A.3 | B.1 | C.-1 | D.-3 |
下列函数中,在其定义域内既是奇函数又是增函数的是
A. | B. | C. | D. |
设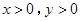 ,定义
,定义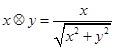 ,则
,则 +2
+2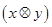
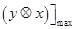 等于( )
等于( )
A.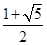 | B.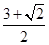 |
C.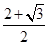 | D.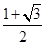 |
已知函数 的定义域为
的定义域为 ,部分对应值如下表,函数
,部分对应值如下表,函数 的大致图像如下图所示,则函数
的大致图像如下图所示,则函数 在区间
在区间 上的零点个数为( )
上的零点个数为( )
 | -2 | 0 | 4 |
 | 0 | -1 | 0 |
设函数f(x)是定义在R上的奇函数,若f(x)的最小正周期为4,且f( 1)>1, 
f(2)=m2-2m,f(3)=  ,则实数m的取值集合是( )
,则实数m的取值集合是( )
A. | B.{O,2} |
C.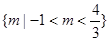 | D.{0} |
设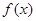 是定义在
是定义在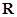 上的奇函数,且当
上的奇函数,且当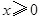 时,
时,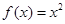 ,若对任意的
,若对任意的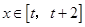 ,不等式
,不等式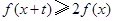 恒成立,则实数
恒成立,则实数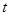 的取值范围是( )
的取值范围是( )
A.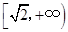 | B.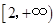 |
C.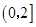 | D.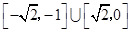 |
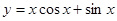 的图象大致为( )
的图象大致为( )