题目内容
(2014·济南模拟)已知函数f(x)= sinωx-sin2
sinωx-sin2 +
+ (ω>0)的最小正周期为π.
(ω>0)的最小正周期为π.
(1)求ω的值及函数f(x)的单调递增区间.
(2)当x∈ 时,求函数f(x)的取值范围.
时,求函数f(x)的取值范围.
 sinωx-sin2
sinωx-sin2 +
+ (ω>0)的最小正周期为π.
(ω>0)的最小正周期为π.(1)求ω的值及函数f(x)的单调递增区间.
(2)当x∈
 时,求函数f(x)的取值范围.
时,求函数f(x)的取值范围. (1) ,k∈Z.
,k∈Z.
(2)
 ,k∈Z.
,k∈Z.(2)

(1)f(x)= sinωx-
sinωx- +
+
= sinωx+
sinωx+ cosωx=sin
cosωx=sin .
.
因为f(x)最小正周期为π,所以ω=2.
所以f(x)=sin .
.
由2kπ- ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ ,k∈Z,
,k∈Z,
得kπ- ≤x≤kπ+
≤x≤kπ+ ,k∈Z.
,k∈Z.
所以函数f(x)的单调递增区间为 ,k∈Z.
,k∈Z.
(2)因为x∈ ,所以2x+
,所以2x+ ∈
∈ ,
,
所以- ≤sin
≤sin ≤1.
≤1.
所以函数f(x)在 上的取值范围是
上的取值范围是 .
.
 sinωx-
sinωx- +
+
=
 sinωx+
sinωx+ cosωx=sin
cosωx=sin .
.因为f(x)最小正周期为π,所以ω=2.
所以f(x)=sin
 .
.由2kπ-
 ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ ,k∈Z,
,k∈Z,得kπ-
 ≤x≤kπ+
≤x≤kπ+ ,k∈Z.
,k∈Z.所以函数f(x)的单调递增区间为
 ,k∈Z.
,k∈Z.(2)因为x∈
 ,所以2x+
,所以2x+ ∈
∈ ,
,所以-
 ≤sin
≤sin ≤1.
≤1.所以函数f(x)在
 上的取值范围是
上的取值范围是 .
.
练习册系列答案
相关题目
 cos(x+π)cosx,(x∈R)
cos(x+π)cosx,(x∈R) =(
=(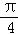 ,
,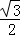 )平移后得到的函数y=g(x)的图象,求y=g(x)在(0,
)平移后得到的函数y=g(x)的图象,求y=g(x)在(0, 、
、 的夹角为
的夹角为 (即
(即 ),现有可供建造第三面围墙的材料
),现有可供建造第三面围墙的材料 米(两面墙的长均大于
米(两面墙的长均大于 ,问当
,问当 为多少时,所建造的三角形露天仓库的面积最大,并求出最大值?
为多少时,所建造的三角形露天仓库的面积最大,并求出最大值? 
 (ω>0)的图像向左平移
(ω>0)的图像向左平移 个单位,得到函数y=g(x)的图象.
个单位,得到函数y=g(x)的图象. 上为增函数,则ω的最大值为________.
上为增函数,则ω的最大值为________.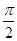 )内递增的是( )
)内递增的是( )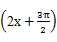 (x∈R),给出下面命题错误的是
(x∈R),给出下面命题错误的是 对称
对称 上是增函数
上是增函数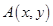 在圆
在圆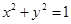 上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周.已知时间
上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周.已知时间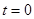 时,
时,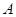 坐标是
坐标是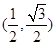 ,则当
,则当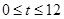 时,动点
时,动点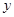 关于
关于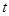 (秒)的函数的单调递增区间是( )
(秒)的函数的单调递增区间是( )


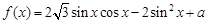 ,
,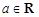 .
.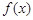 的最小正周期;
的最小正周期;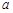 的取值范围.
的取值范围.