题目内容
求y=|3x-x3|在[-2,2]上的最大值及最小值.
解:∵![]() =y=|3x-x3|=|x|·|3-x2|满足f(-x)=
=y=|3x-x3|=|x|·|3-x2|满足f(-x)= ![]() 为偶函数,
为偶函数,
∴只需考查其在[0,2]上的最大值或最小值.
又![]() =|3x-x3|
=|3x-x3|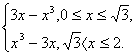
故![]() =
=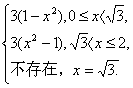
令![]() =0,得x=1.
=0,得x=1.
∵f(0)=0,f(2)=2,f(![]() )=0,f(1)=2,
)=0,f(1)=2,
∴![]() 在[0,2]上的最大值为2,最小值为0.
在[0,2]上的最大值为2,最小值为0.
点评:化简是解决复杂问题的基本途径.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目