题目内容

若（1-x-1）2009=a0+a1x-1+L+a2009x-2009，2a1+22a1+L+22009a2009值为
-2
-2
．
分析：给二项展开式中的x赋值
1
2
；求出a0+2a1+22a2+…+22009a2009的值；利用二项展开式的通项公式求出常数项；求出2a1+22a2+…+22009a2009的值．
解答：解：令x=
1
2
得
a0+2a1+22a2+…+22009a2009=-1
∵a0=1
∴2a1+22a2+…+22009a2009=-2
故答案为-2
点评：本题考查通过给二项展开式的x赋值求展开式的系数和、考查利用二项展开式的通项公式求特定项．
练习册系列答案
相关题目
已知命题p：?x∈[1，12]，x2-a≥0．命题q：?x0∈R，使得x
 
2
0
+（a-1）x0+1＜0．
（1）若p或q为真，p且q为假，求实数a的取值范围． 
（2）实数m分别取什么值时，复数z=m+1+（m-1）i是 ①实数？②虚数？③纯虚数？
若方程
|x2-1|x-1
=kx有两个实数根，则实数k的取值范围是
0＜k＜1或1＜k＜2
0＜k＜1或1＜k＜2
．
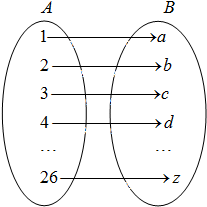设f是由集合A={x|x∈N，且1≤x≤26}到B={a，b，c，…，z}（即26个英文字母按照字母表顺序排列）的映射，集合B中的任何一个元素在A中也只有唯一的元素与之对应，其对应法则如图所示（依次对齐）；又知函数g（x）=
log232-x，(22＜x＜32)
x+4，(0≤x≤22)
，
若f（x1），f[g（20）]，f[g（x2）]，f[g（9）]所表示的字母依次排列组成的英文单词为exam，则x1+x2=
35
35
．
已知函数f（x）=
x
m
-1(x≥1)
log
1
2
(1-x)(x＜1)
若f[f（
3
4
）]＞0，则m的取值范围是
0＜m＜2
0＜m＜2
．
下列四个命题中，正确的有（　　）
①两个变量间的相关系数γ越小，说明两变量间的线性相关程度越低；
②命题P：“?x0∈R，x
 
2
0
-x0-1＞0”的否定?P：“?x∈R，x2-x-1＜0”；
③用相关指数R2来刻画回归效果，若R2越大，则说明模型的拟合效果越好；
④若a=0.32，b=20.3，c=log0.32，则c＜a＜b．
A、①③④B、①④C、③④D、②③

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网