题目内容
在数列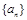 中,
中,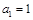 ,且对任意的
,且对任意的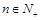 ,都有
,都有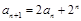 .
.
(1)求证:数列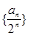 是等差数列;
是等差数列;
(2)设数列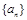 的前
的前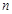 项和为
项和为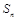 ,求证:对任意的
,求证:对任意的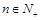 ,
,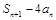 都为定值.
都为定值.
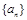 中,
中,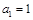 ,且对任意的
,且对任意的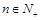 ,都有
,都有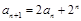 .
.(1)求证:数列
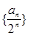 是等差数列;
是等差数列;(2)设数列
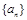 的前
的前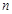 项和为
项和为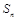 ,求证:对任意的
,求证:对任意的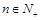 ,
,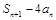 都为定值.
都为定值.证明: (1)∵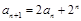 ,∴
,∴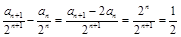 .
.
∴数列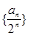 是以
是以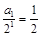 为首项,
为首项,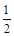 为公差的等差数列.
为公差的等差数列.
(2) 由(1)知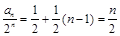 ,∴
,∴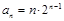 .
.
∴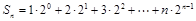 .…………………………①
.…………………………①
∴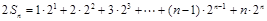 .……………………………………②
.……………………………………②
∴由②-①可得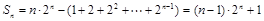 .
.
∴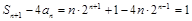 ,故结论成立.
,故结论成立.
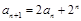 ,∴
,∴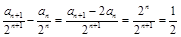 .
.∴数列
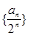 是以
是以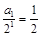 为首项,
为首项,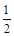 为公差的等差数列.
为公差的等差数列.(2) 由(1)知
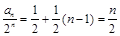 ,∴
,∴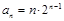 .
.∴
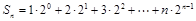 .…………………………①
.…………………………①∴
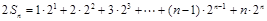 .……………………………………②
.……………………………………②∴由②-①可得
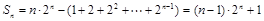 .
.∴
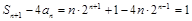 ,故结论成立.
,故结论成立.本试题考查了等差数列的定义的运用以及运用错位相减法来求解数列和的综合运用试题,以及恒等式的证明。

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
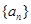 是一个等差数列,且
是一个等差数列,且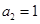 ,
,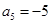 。
。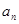 ;
;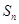 的最大值.
的最大值.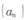 的前n项和为
的前n项和为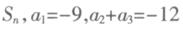 ,则使
,则使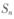 取得最小值时n的值为
取得最小值时n的值为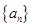 的前
的前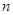 项和为
项和为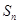 ,且对任意的
,且对任意的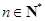 ,都有
,都有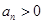 ,
,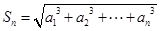 .
.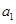 ,
,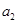 的值;
的值;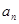
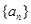 的首项
的首项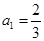 ,
,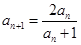 ,
,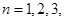 ….
….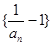 是等比数列; (Ⅱ)求数列
是等比数列; (Ⅱ)求数列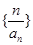 的前
的前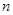 项和
项和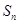
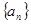 的前
的前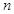 项和为
项和为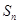 ,若
,若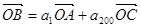 ,且
,且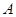 、
、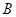 、
、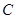 三点共线(该直线不过点
三点共线(该直线不过点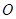 ),则
),则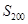 等于( )
等于( )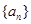 不是常数列,且
不是常数列,且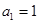 ,若
,若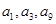 构成等比数列.
构成等比数列.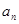 ;
;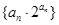 前n项和
前n项和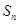
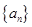 中,首项
中,首项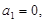 公差
公差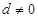 ,若
,若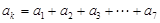 ,则
,则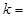 ( )
( )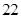
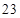
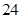
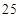
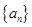 的前
的前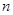 项和为
项和为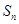 ,若
,若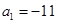 ,
,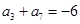 ,则当
,则当