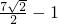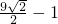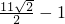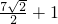Question

若曲线y=－x³+3与直线y=－6x+b相切,则b为__________.

Answer 1

3±4

解析:

本题考查导数的几何意义.关键是确定曲线上哪一点的导数等于－6.

y′=－3x².

令y′=－3x²=－6,得x=±.

把x=代入曲线方程中,得y=3－2.

把x=－代入曲线方程中,得y=3+2.

因为曲线与直线y=－6x+b相切,所以切点也在直线y=－6x+b上.

分别把(,3－2)、(－,3+2)代入直线方程中,得b₁=3+4,b₂=3－4.