题目内容
设椭圆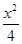 +y2=1的左焦点为F,P为椭圆上一点,其横坐标为
+y2=1的左焦点为F,P为椭圆上一点,其横坐标为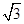 ,则|PF|等于( )
,则|PF|等于( )
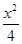 +y2=1的左焦点为F,P为椭圆上一点,其横坐标为
+y2=1的左焦点为F,P为椭圆上一点,其横坐标为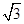 ,则|PF|等于( )
,则|PF|等于( )A. | B. | C. | D.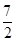 |
D
设P(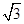 ,y),
,y),
由 +y2=1,
+y2=1,
解得y2= .
.
由椭圆方程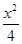 +y2=1知a=2,b=1.
+y2=1知a=2,b=1.
∴c=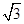 ,F(-
,F(-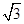 ,0),
,0),
∴|PF|=
=
=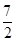 .
.
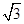 ,y),
,y),由
 +y2=1,
+y2=1,解得y2=
 .
.由椭圆方程
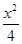 +y2=1知a=2,b=1.
+y2=1知a=2,b=1.∴c=
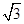 ,F(-
,F(-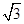 ,0),
,0),∴|PF|=

=

=
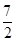 .
.
练习册系列答案
相关题目
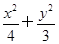 =1的中心和左焦点,点P为椭圆上的任意一点,则
=1的中心和左焦点,点P为椭圆上的任意一点,则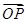 ·
·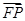 的最大值为________.
的最大值为________.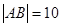 ,图中的一系列圆是圆心分别为A、B的两组同心圆,每组同心圆的半径分别是1,2,3,…,n,…. 利用这两组同心圆可以画出以A、B为焦点的椭圆或双曲线. 若其中经过点M、N的椭圆的离心率分别是
,图中的一系列圆是圆心分别为A、B的两组同心圆,每组同心圆的半径分别是1,2,3,…,n,…. 利用这两组同心圆可以画出以A、B为焦点的椭圆或双曲线. 若其中经过点M、N的椭圆的离心率分别是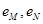 ,经过点P,Q 的双曲线的离心率分别是
,经过点P,Q 的双曲线的离心率分别是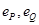 ,则它们的大小关系是 (用“
,则它们的大小关系是 (用“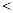 ”连接)
”连接)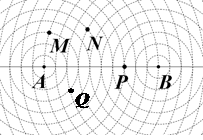
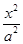 +
+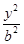 =1(a>b>0)的两个焦点.
=1(a>b>0)的两个焦点.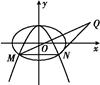
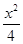 +y2=1与双曲线C2的公共焦点,A,B分别是C1,C2在第二、四象限的公共点.若四边形AF1BF2为矩形,则C2的离心率是( )
+y2=1与双曲线C2的公共焦点,A,B分别是C1,C2在第二、四象限的公共点.若四边形AF1BF2为矩形,则C2的离心率是( )




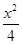 +
+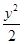 =1的两个焦点是F1、F2,点P在该椭圆上,若|PF1|-|PF2|=2,则△PF1F2的面积是 .
=1的两个焦点是F1、F2,点P在该椭圆上,若|PF1|-|PF2|=2,则△PF1F2的面积是 .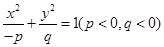 表示双曲线,那么下列椭圆中,与这个双曲线共焦点的是( )
表示双曲线,那么下列椭圆中,与这个双曲线共焦点的是( )


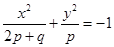
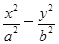 =1和椭圆
=1和椭圆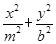 =1(a>0,m>b>0)的离心率互为倒数,那么以a,b,m为边长的三角形是( )
=1(a>0,m>b>0)的离心率互为倒数,那么以a,b,m为边长的三角形是( )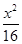 +
+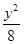 =1的离心率为( )
=1的离心率为( )