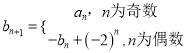题目内容
【题目】已知曲线![]() .
.
(1)若曲线C在点![]() 处的切线为
处的切线为![]() ,求实数
,求实数![]() 和
和![]() 的值;
的值;
(2)对任意实数![]() ,曲线
,曲线![]() 总在直线
总在直线![]() :
:![]() 的上方,求实数
的上方,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
,![]() ,(2)
,(2)![]() .
.
【解析】
试题分析:(1)根据导数几何意义,所以![]() .因为
.因为![]() ,所以
,所以![]() .因为
.因为![]() 过点
过点![]() ,所以
,所以![]() ,(2)由题意得:不等式
,(2)由题意得:不等式![]() 恒成立,恒成立问题一般转化为最值问题.一是分类讨论求函数
恒成立,恒成立问题一般转化为最值问题.一是分类讨论求函数![]() 最小值,二是变量分离为
最小值,二是变量分离为![]() 恒成立,求函数
恒成立,求函数![]() 最小值.两种方法都是
最小值.两种方法都是![]() ,然后对实数a进行讨论,当
,然后对实数a进行讨论,当![]() 时,
时,![]() ,所以
,所以![]() .当
.当![]() 时,由
时,由![]() 得
得![]() ,不论
,不论![]() 还是
还是![]() ,
,![]() 都是先减后增,即
都是先减后增,即![]() 的最小值为
的最小值为![]() ,所以
,所以![]() .
.
试题解析:解
(1)![]() , 2分
, 2分
因为曲线C在点(0,1)处的切线为L:![]() ,
,
所以![]() 且
且![]() . 4分
. 4分
解得![]() ,
,![]() -5分
-5分
(2)法1:
对于任意实数a,曲线C总在直线的![]() 的上方,等价于
的上方,等价于
x,![]() ,都有
,都有![]() ,
,
即x,![]() R,
R,![]() 恒成立, 6分
恒成立, 6分
令![]() , 7分
, 7分
①若a=0,则![]() ,
,
所以实数b的取值范围是![]() ; 8分
; 8分
②若![]() ,
,![]() ,
,
由![]() 得
得![]() , 9分
, 9分
![]() 的情况如下:
的情况如下:
|
| 0 |
|
|
| 0 | + |
|
| 极小值 |
|
11分
所以![]() 的最小值为
的最小值为![]() , 12分
, 12分
所以实数b的取值范围是![]() ;
;
综上,实数b的取值范围是![]() . 13分
. 13分
法2:对于任意实数a,曲线C总在直线的![]() 的上方,等价于
的上方,等价于
x,![]() ,都有
,都有![]() ,即
,即
x,![]() R,
R,![]() 恒成立, 6分
恒成立, 6分
令![]() ,则等价于
,则等价于![]() ,
,![]() 恒成立,
恒成立,
令![]() ,则
,则![]() , 7分
, 7分
由![]() 得
得![]() , 9分
, 9分
![]() 的情况如下:
的情况如下:
|
| 0 |
|
|
| 0 | + |
|
| 极小值 |
|
-11分
所以![]() 的最小值为
的最小值为![]() , 12分
, 12分
实数b的取值范围是![]() . 13分
. 13分

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目