题目内容
已知向量 ,
, 都是非零向量,若
都是非零向量,若 垂直,
垂直, 垂直,则
垂直,则 与
与 的夹角为( )
的夹角为( )
A B
B  C
C  D
D 
 ,
, 都是非零向量,若
都是非零向量,若 垂直,
垂直, 垂直,则
垂直,则 与
与 的夹角为( )
的夹角为( )A
 B
B  C
C  D
D 
D
由
 垂直,可得
垂直,可得 ,则
,则 ①,同理,
①,同理, 垂直,可得
垂直,可得 ,即
,即 ②,①―②,得
②,①―②,得 ,代入①,得
,代入①,得 ,所以
,所以 ,则
,则 与
与 的夹角余弦值为
的夹角余弦值为 ,所以夹角为
,所以夹角为 .
.点评:此题难度不大,主要是计算较多,考点比较清晰.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
 且
且 ∥
∥ ,则
,则 为: ( )
为: ( )




 满足
满足 ,
, 与
与 的夹角为600,则
的夹角为600,则 的值为( )
的值为( )


 的值.
的值.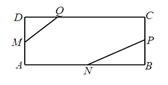
 ,
, ,
, 与
与 的夹角
的夹角 ,则向量
,则向量





 ,
, ,则
,则 在
在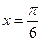 ,求向量a,c的夹角;
,求向量a,c的夹角;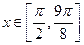 时,求函数f(x)=2a·b+1的最大值。
时,求函数f(x)=2a·b+1的最大值。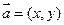 ,
,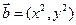 ,
,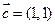 ,
,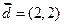 ,且
,且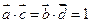 ,则起点在原点的向量
,则起点在原点的向量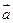 的个数为 .
的个数为 .