题目内容
本小题满分13分)已知椭圆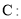
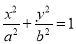 (
(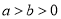 )的右焦点与抛物线
)的右焦点与抛物线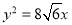 的焦点重合,且椭圆
的焦点重合,且椭圆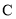 的离心率
的离心率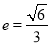 .
.
(1)求椭圆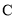 的标准方程;
的标准方程;
(2)若直线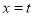 (
(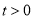 )与椭圆
)与椭圆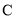 交于不同的两点
交于不同的两点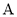 ,
,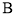 ,以线段
,以线段 为直径作圆
为直径作圆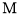 .若圆
.若圆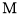 与
与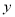 轴相切,求直线
轴相切,求直线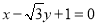 被圆
被圆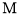 所截得的弦长.
所截得的弦长.
(I)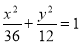 ;(2)
;(2)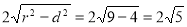 .
.
【解析】
试题分析:(1)抛物线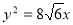 的焦点坐标为
的焦点坐标为 ,得到
,得到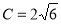 ;
;
根据椭圆的离心率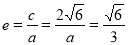 ,得到
,得到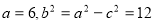
即可得到椭圆方程.
(2)由题意知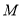 ,圆心
,圆心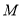 为线段
为线段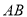 中点,且位于
中点,且位于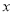 轴的正半轴,
轴的正半轴,
设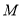 的坐标为
的坐标为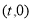
根据圆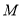 与
与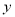 轴相切,不妨设点
轴相切,不妨设点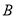 在第一象限,又
在第一象限,又 ,得到
,得到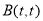
进一步得到圆心、半径、圆的方程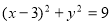
根据圆心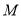 到直线
到直线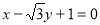 的距离
的距离
利用“圆的特征三角形”确定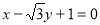 被圆
被圆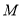 所截得的弦长.
所截得的弦长.
试题解析:(1)因为抛物线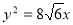 的焦点坐标为
的焦点坐标为 ,所以
,所以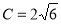 2分
2分
又椭圆的离心率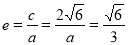 ,所以
,所以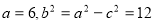
所以椭圆方程为: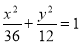 5分
5分
(2)由题意知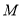 ,圆心
,圆心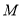 为线段
为线段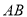 中点,且位于
中点,且位于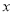 轴的正半轴,
轴的正半轴,
故设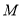 的坐标为
的坐标为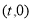
因为圆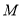 与
与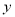 轴相切,不妨设点
轴相切,不妨设点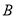 在第一象限,又
在第一象限,又 ,所以
,所以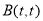
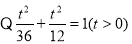 解得
解得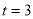 8分
8分
 圆心
圆心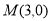 ,半径
,半径
 圆
圆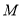 的方程为:
的方程为: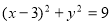 10分
10分
又圆心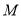 到直线
到直线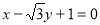 的距离
的距离
所以,直线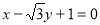 被圆
被圆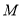 所截得的弦长为:
所截得的弦长为:
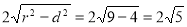 13分
13分
考点:1.椭圆的标准方程及其几何性质;2.抛物线的几何性质;3.直线与圆的位置关系.
考点分析: 考点1:椭圆的标准方程 考点2:椭圆的几何性质 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 中,侧棱垂直于底面,点
中,侧棱垂直于底面,点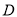 是
是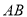 的中点.
的中点.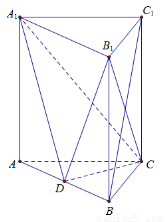
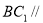 平面
平面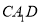 ;
;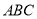 为边长为
为边长为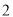 的正三角形,
的正三角形,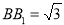 ,求三棱锥
,求三棱锥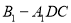 的体积.
的体积.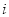 是虚数单位,复数
是虚数单位,复数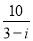 在复平面内表示的点在( )
在复平面内表示的点在( ) ,
, ,则
,则 等于( )
等于( ) B.
B.
 D.
D.
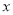 轴的正半轴为极轴建立极坐标系.已知直线
轴的正半轴为极轴建立极坐标系.已知直线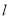 的极坐标方程为
的极坐标方程为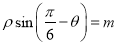 (
(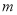 为常数),圆
为常数),圆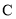 的参数方程为
的参数方程为 (
(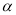 为参数).
为参数).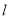 的直角坐标方程和圆
的直角坐标方程和圆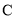 的普通方程;
的普通方程;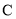 关于直线
关于直线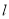 的对称点亦在圆上,求实数
的对称点亦在圆上,求实数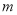 的值.
的值.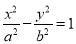 (
(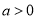 ,
,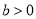 )的一个焦点
)的一个焦点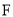 作一条渐近线的垂线,若垂足恰在线段
作一条渐近线的垂线,若垂足恰在线段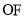 (
(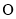 为坐标原点)的垂直平分线上,则双曲线的离心率为 .
为坐标原点)的垂直平分线上,则双曲线的离心率为 .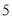 次月考的数学成绩统计如茎叶图所示,若甲、乙两人的平均成绩分别是
次月考的数学成绩统计如茎叶图所示,若甲、乙两人的平均成绩分别是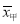 、
、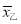 ,则下列正确的是( )
,则下列正确的是( )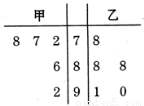
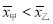 ,甲比乙成绩稳定
,甲比乙成绩稳定 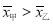 ,乙比甲成绩稳定
,乙比甲成绩稳定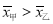 ,甲比乙成绩稳定
,甲比乙成绩稳定  ,则
,则 的值为 .
的值为 . 集合
集合 ,集合
,集合 ,则集合
,则集合 的面积为 .
的面积为 .