题目内容
(本小题满分12分)设关于 的方程
的方程 ,
,
(1)若方程有实数解,求实数 的取值范围;
的取值范围;
(2)当方程有实数解时,讨论方程实根的个数,并求出方程的解。
(1) ),(2)1)当
),(2)1)当 时原方程有两解,
时原方程有两解, ;2)当
;2)当 或
或 时,原方程有唯一解
时,原方程有唯一解 ;3)当
;3)当 时,原方程无解。
时,原方程无解。
【解析】
试题分析:关于 的方程
的方程 有实数解问题,可以转化
有实数解问题,可以转化 与
与 的图象有交点即可,因
的图象有交点即可,因
 ,只需
,只需 即可,第二步依据
即可,第二步依据 ,由于
,由于 时有实数解,所以对
时有实数解,所以对 分
分 和
和 进行讨论,研究方程根的个数并求出相应的跟.
进行讨论,研究方程根的个数并求出相应的跟.
试题解析:(1)∵ ,∴当
,∴当 时方程有实数解;
时方程有实数解;
(2)①当 时,
时, ,∴方程有唯一解
,∴方程有唯一解 ;
;
②当 时,∵
时,∵ ,
,
∵ ,∴
,∴ 的解为
的解为 ;
;
令 ,
,
∴当 时,
时, 的解为
的解为 ;
;
综合①、②,得
1)当 时原方程有两解,
时原方程有两解, ;
;
2)当 或
或 时,原方程有唯一解
时,原方程有唯一解 ;
;
3)当 时,原方程无解。
时,原方程无解。
考点:1.换元法;2.二次函数值域;解指数方程;

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
 ,圆
,圆 的面积为
的面积为 ,则
,则 .
.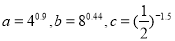 ,则 ( )
,则 ( ) ,则实数
,则实数 的值等于 .
的值等于 .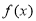 与
与 的各组中,是同一个关于x的函数的是( )
的各组中,是同一个关于x的函数的是( )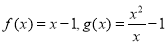
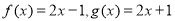
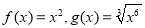

 ,则函数
,则函数 的奇偶性为__________
的奇偶性为__________ 是定义在区间
是定义在区间 上的奇函数,则
上的奇函数,则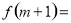 ( )
( )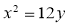 的焦点为
的焦点为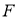 ,经过点
,经过点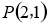 的直线
的直线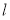 与抛物线相交于
与抛物线相交于 两点且点
两点且点 恰为
恰为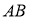 的中点,则
的中点,则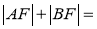 .
. 一个正三菱柱的左视图是边长为2
一个正三菱柱的左视图是边长为2