题目内容
对于函数![]() ,如果存在实数
,如果存在实数![]() 使得
使得![]() ,那么称
,那么称![]() 为
为![]() 的生成函数.
的生成函数.
(1)下面给出两组函数,![]() 是否分别为
是否分别为![]() 的生成函数?并说明理由;
的生成函数?并说明理由;
第一组:![]() ;
;
第二组:![]() ;
;
(2)设![]() ,生成函数
,生成函数![]() .若不等式
.若不等式
![]() 在
在![]() 上有解,求实数
上有解,求实数![]() 的取值范围;
的取值范围;
(3)设![]() ,取
,取![]() ,生成函数
,生成函数![]() 使
使![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
解:(1)① 设![]() ,即
,即![]() ,取
,取![]() ,所以
,所以![]() 是
是![]() 的生成函数.……………………2分
的生成函数.……………………2分
② 设![]() ,即
,即![]() ,
,
则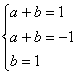 ,该方程组无解.所以
,该方程组无解.所以![]() 不是
不是![]() 的生成函数.………4分
的生成函数.………4分
(2)![]() …………………………5分
…………………………5分
若不等式![]() 在
在![]() 上有解,
上有解,
![]() ,即
,即![]() ……7分
……7分
设![]() ,则
,则![]() ,
,![]() ,……9分
,……9分
![]() ,故,
,故,![]() .………………………………………………………10分
.………………………………………………………10分
(3)(解法一)由题意,![]() 对一切
对一切![]() 恒成立。
恒成立。
即![]() 对一切
对一切![]() 恒成立。
恒成立。
当![]() 时,
时,![]() 恒成立,此时
恒成立,此时![]() ;
;
当![]() 时,
时,![]() 恒成立,
恒成立,![]() 可得
可得![]() ,故
,故![]() ;
;
又![]() ,综上可知,
,综上可知,![]() …………………18分
…………………18分
(解法二)由题意,得![]()
![]() 若
若![]() ,则
,则![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,
上递增,
则![]() ,所以
,所以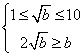 ,得
,得![]()
![]() 若
若![]() ,则
,则![]() 在
在![]() 上递增,则
上递增,则![]() ,
,
所以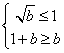 ,得
,得![]() .
.
![]() 若
若![]() ,则
,则![]() 在
在![]() 上递减,则
上递减,则![]() ,
,
故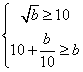 ,无解
,无解
综上可知,![]() ………………………………………………………18分
………………………………………………………18分

练习册系列答案
相关题目
 )的值;
)的值;