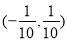题目内容
(本小题满分14分) 已知函数函数

(1)判断并证明函数 的奇偶性;
的奇偶性;
(2)证明函数 在
在 上是增函数。
上是增函数。
(3)若 >2,求
>2,求 的取值范围。
的取值范围。
(1)奇函数(2)同解析(3)  且
且
【解析】
试题分析:(1)对于判断函数奇偶性,通常利用定义法。分两步1)先求定义域,2)计算 (2)证明函数的单调性可利用定义法,先设,再作差,最后定号。(3)先把
(2)证明函数的单调性可利用定义法,先设,再作差,最后定号。(3)先把 代入 ,然后解不等式。另本题给出的函数是对勾函数,可给学生补充对勾函数的有关知识。
代入 ,然后解不等式。另本题给出的函数是对勾函数,可给学生补充对勾函数的有关知识。
试题解析:(1) 的定义域为
的定义域为 ,
, 
∴函数 为奇函数 ( 4分 )
为奇函数 ( 4分 )
(2)任取 ,不妨设
,不妨设 ,则有
,则有

∵ 且
且 ∴
∴ ,
, ,
,
∴ 即
即 ∴函数
∴函数 在
在 上是增函数.(10分)
上是增函数.(10分)
(3)若 即
即 ,显然
,显然 , 原式可化为:
, 原式可化为: 解得
解得 且
且
(14分)
考点:奇偶性,单调性的判断,解不等式

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 与直线
与直线 平行,则它们之间的距离是( )
平行,则它们之间的距离是( ) D.4
D.4 =3,
=3, =3.5,则由
=3.5,则由 =-2x+9.5 B.
=-2x+9.5 B. =2x-2.4
=2x-2.4 =0.4x+2.3 D.
=0.4x+2.3 D. =-0.3x+4.4
=-0.3x+4.4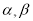 是两个不同的平面,
是两个不同的平面,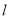 是一条直线,以下命题正确的是( )
是一条直线,以下命题正确的是( )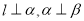 ,则
,则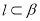
 ,则
,则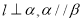 ,则
,则
 ,则
,则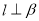
 的定义域是 ( )
的定义域是 ( ) B.
B. C.
C. D.
D.
 是偶函数,则k的值是
是偶函数,则k的值是  B.
B. C.
C. D.
D.
 的部分图象如图所示,若
的部分图象如图所示,若 ,则
,则 等于( )
等于( )
 B.
B. C.
C. D.
D.
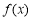 是定义在R上的奇函数,它的图象关于直线
是定义在R上的奇函数,它的图象关于直线 对称,且
对称,且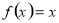
 .若函数
.若函数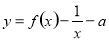 在区间
在区间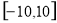 上有10个零点(互不相同),则实数
上有10个零点(互不相同),则实数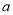 的取值范围是
的取值范围是 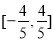 B.
B.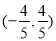 C.
C. D.
D.