Question

已知直线l:x+y-2=0,一束光线过点P(0,+1),以120°的倾斜角投射到l上,经过l反射,求反射光线所在直线的方程.

Answer 1

解法一：如下图,设入射光线交l于Q点,交x轴于M点,反射光线交x轴于P₂点,l交x轴于N点.

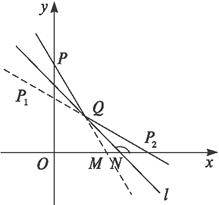
∵∠QMP₂=120°,∠QNP₂=135°,

∴∠MQN=15°.

由光的反射定理知∠MQN=∠NQP₂=15°,故反射光线的倾斜角θ=120°+30°=150°.

∴所求直线的斜率为-.

由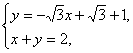得Q(1,1).

故反射光线所在直线的方程为y-1=-(x-1),

即x+y--1=0.

解法二:k_λ=-,设反射光线的斜率为k,由入射光线到l的角等于l到反射光线的角,所以有.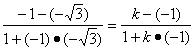

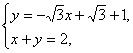解之,得k=-.由得Q(1,1).

故反射光线所在直线的方程为y-1=-(x-1),即x+y--1=0.

解法三:设P(0, +1)关于l的对称点是P′(x′,y′),

则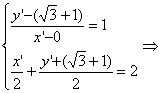P′(1-,2).

又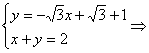Q(1,1).

由两点式得反射光线所在直线的方程为x+y--1=0.