题目内容

求实数m的取值范围，使抛物线y=x2上存在两点关于直线y=m(x-3)对称.

分析：设出对称两点坐标，利用其中点在对称轴上来求解.

解：设抛物线上两点A（x1,y1），B（x2,y2）关于直线y=m(x-3)对称，AB的中点为M（x0,y0）.

显然m≠0，则kAB==x1+x2=.①

所以x0=,y0==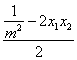，将x0,y0代入方程y=m(x-3),

解得x1x2=+3m.②

由①②知x1、x2是方程x2+x+(+3m)=0的两根，由Δ＞0可解得m＜.

点拨：要使抛物线上存在两点关于所给直线对称，必须保证两个交点的连线段被所给直线垂直平分.

练习册系列答案
相关题目
设f（x）=log 
1
2
1-ax
x-1
（a为常数）的图象关于原点对称
（1）求a的值；
（2）判断函数f（x）在区间（1，+∞）的单调性并证明；
（3）若对于区间[3，4]上的每一个x的值，f（x）＞（
1
2
）x+m恒成立，求实数m的取值范围．
已知函数f（x）满足f(x)=ln
1+x1-x
，
（1）求f（x）的定义域；判断f（x）的奇偶性及单调性并给予证明；
（2）对于函数f（x），当x∈（-1，1）时，f（1-m）+f（1-m2）＜0．求实数m的取值范围．
已知函数f（x）=Asin（ωx+?）（A＞0，ω＞0，|?|＜
π2
）在一个周期内的图象如下图所示．
（1）求函数的解析式；
（2）求函数的单调递增区间；
（3）设0＜x＜π，且方程f（x）=m有两个不同的实数根，求实数m的取值范围．
已知函数f(x)=
x-ax-2

（1）若a∈N*，且函数f（x）在区间（2，+∞）上是减函数，求a的值；
（2）若a∈R，且关于x的方程f（x）=-x有且只有一根落在区间（-2，-1）内，求a的取值范围；
（3）在（1）的条件下，若对于区间[3，4]上的每一个x的值，不等式f（x）＞m-x-3恒成立，求实数m的取值范围．
已知中心在坐标原点，对称轴为坐标轴的椭圆经过两点A(0，-3)、B(
3
，
3
2
)．
（1）求此椭圆的标准方程； 
（2）若点（-1，m）恰在此椭圆内部，求实数m的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网