题目内容
已知递增等差数列{an}公差为d,正项等比数列{bn}公比为q,(q≠1),是否存在实数m,使得logm
与n无关?若存在,求出m,若不存在,说明理由.
| bn | man |
分析:由d>0,q>0,q≠1,知logm
=logmbn-an=logmb1qn-1-[a1+(n-1)d]=(-a1+logmb1)+(n-1)(logmq-d),要使其与n无关,只需logmq-d=0,由此能求出m.
| bn |
| man |
解答:解:∵d>0,q>0,q≠1,
∴logm
=logmbn-an=logmb1qn-1-[a1+(n-1)d]
=(-a1+logmb1)+(n-1)(logmq-d),
要使其与n无关,
只需logmq-d=0,
即m=q
,
此时∵q>0,q≠1,
∴m>0,m≠1,满足要求的m存在,
为m=q
.
∴logm
| bn |
| man |
=(-a1+logmb1)+(n-1)(logmq-d),
要使其与n无关,
只需logmq-d=0,
即m=q
| 1 |
| d |
此时∵q>0,q≠1,
∴m>0,m≠1,满足要求的m存在,
为m=q
| 1 |
| d |
点评:本题考查等差数列的通项公式,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 .
. 成等差数列,且
成等差数列,且 =9,求a的值.
=9,求a的值.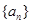 中,
中,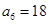 且
且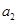 是
是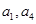 的等比中项,则它的第4项到第11项的和为
的等比中项,则它的第4项到第11项的和为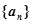 ,满足
,满足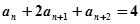 ,则该数列为( )
,则该数列为( )