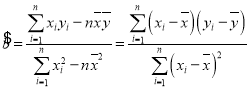题目内容
【题目】设函数![]() ,
,![]() (
(![]() ).
).
(1)当![]() 时,解关于
时,解关于![]() 的方程
的方程![]() (其中
(其中![]() 为自然对数的底数);
为自然对数的底数);
(2)求函数![]() 的单调增区间;
的单调增区间;
(3)当![]() 时,记
时,记![]() ,是否存在整数
,是否存在整数![]() ,使得关于
,使得关于![]() 的不等式
的不等式![]() 有解?若存在,请求出
有解?若存在,请求出![]() 的最小值;若不存在,请说明理由. (参考数据:
的最小值;若不存在,请说明理由. (参考数据:![]() ,
,![]() )
)
【答案】(Ⅰ)![]() 或
或![]() (Ⅱ)当
(Ⅱ)当![]() 时,
时,![]() 的增区间为
的增区间为![]() ;当
;当![]() 时,
时,![]() 的增区间为
的增区间为![]() ;
;![]() 时,
时,![]() 的增区间为
的增区间为![]() .(III)
.(III)![]() 的最小值为
的最小值为![]() .
.
【解析】
试题分析:(Ⅰ)代入化简方程得![]() ,由二次方程解得
,由二次方程解得![]() 或
或![]() ,再根据指对数关系得
,再根据指对数关系得![]() 或
或![]() .(Ⅱ)先求函数导数并明确函数定义域:
.(Ⅱ)先求函数导数并明确函数定义域:![]() ,
,![]() ;再讨论导函数不变号情况:当
;再讨论导函数不变号情况:当![]() 时,
时,![]() ,
,![]() 的增区间为
的增区间为![]() ;最后讨论导函数变号时符号变化规律:当
;最后讨论导函数变号时符号变化规律:当![]() 时,由
时,由![]() ,解得
,解得![]() ;当
;当![]() 时,由
时,由![]() ,解得
,解得![]() .(III)存在性问题,一般转化为对应函数最值问题:
.(III)存在性问题,一般转化为对应函数最值问题:![]() ,利用导数先求函数
,利用导数先求函数![]() 最小值:本题难点是最小值点
最小值:本题难点是最小值点![]() 不能解出,只能得到其所在区间,为使
不能解出,只能得到其所在区间,为使![]() 值能确定最小值,需精确考虑最小值点所在区间,如
值能确定最小值,需精确考虑最小值点所在区间,如![]() 细化到
细化到![]()
试题解析:解:(1)当![]() 时,方程
时,方程![]() 即为
即为![]() ,去分母,得
,去分母,得
![]() ,解得
,解得![]() 或
或![]() , …………2分
, …………2分
故所求方程的根为![]() 或
或![]() . ………4分
. ………4分
(2)因为![]() ,
,
所以![]() (
(![]() ), ……6分
), ……6分
①当![]() 时,由
时,由![]() ,解得
,解得![]() ;
;
②当![]() 时,由
时,由![]() ,解得
,解得![]() ;
;
③当![]() 时,由
时,由![]() ,解得
,解得![]() ;
;
④当![]() 时,由
时,由![]() ,解得
,解得![]() ;
;
⑤当![]() 时,由
时,由![]() ,解得
,解得![]() .
.
综上所述,当![]() 时,
时,![]() 的增区间为
的增区间为![]() ;
;
当![]() 时,
时,![]() 的增区间为
的增区间为![]() ;
;
![]() 时,
时,![]() 的增区间为
的增区间为![]() . ………10分
. ………10分
(3)方法一:当![]() 时,
时,![]() ,
,![]() ,
,
所以![]() 单调递增,
单调递增,![]() ,
,![]() ,
,
所以存在唯一![]() ,使得
,使得![]() ,即
,即![]() , ……………12分
, ……………12分
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以![]() ,
,
记函数![]() ,则
,则![]() 在
在![]() 上单调递增, ……14分
上单调递增, ……14分
所以![]() ,即
,即![]() ,
,
由![]() ,且
,且![]() 为整数,得
为整数,得![]() ,
,
所以存在整数![]() 满足题意,且
满足题意,且![]() 的最小值为
的最小值为![]() . ………16分
. ………16分
方法二:当![]() 时,
时,![]() ,所以
,所以![]() ,
,
由![]() 得,当
得,当![]() 时,不等式
时,不等式![]() 有解, ……………12分
有解, ……………12分
下证:当![]() 时,
时,![]() 恒成立,即证
恒成立,即证![]() 恒成立.
恒成立.
显然当![]() 时,不等式恒成立,
时,不等式恒成立,
只需证明当![]() 时,
时,![]() 恒成立.
恒成立.
即证明![]() .令
.令![]() ,
,
所以![]() ,由
,由![]() ,得
,得![]() , ………14分
, ………14分
当![]() ,
,![]() ;当
;当![]() ,
,![]() ;
;
所以![]() .
.
所以当![]() 时,
时,![]() 恒成立.
恒成立.
综上所述,存在整数![]() 满足题意,且
满足题意,且![]() 的最小值为
的最小值为![]() . .……………16分
. .……………16分

【题目】2016年“一带一路”沿线64个国家GDP之和约为12.0万亿美元,占全球GDP的![]() ;人口总数约为32.1亿,占全球总人口的
;人口总数约为32.1亿,占全球总人口的![]() ;对外贸易总额(进口额+出口额)约为71885.6亿美元,占全球贸易总额的
;对外贸易总额(进口额+出口额)约为71885.6亿美元,占全球贸易总额的![]() .
.
2016年“一带一路”沿线国家情况
人口(万人) | GDP(亿美元) | 进口额(亿美元) | 出口额(亿美元) | |
蒙古 | 301.4 | 116.5 | 38.7 | 45.0 |
东南亚11国 | 63852.5 | 25802.2 | 11267.2 | 11798.6 |
南亚8国 | 174499.0 | 29146.6 | 4724.1 | 3308.5 |
中亚5国 | 6946.7 | 2254.7 | 422.7 | 590.7 |
西亚、北非19国 | 43504.6 | 36467.5 | 9675.5 | 8850.7 |
东欧20国 | 32161.9 | 26352.1 | 9775.5 | 11388.4 |
关于“一带一路”沿线国家2016年状况,能够从上述资料中推出的是( )
A.超过六成人口集中在南亚地区
B.东南亚和南亚国家GDP之和占全球的![]() 以上
以上
C.平均每个南亚国家对外贸易额超过1000亿美元
D.平均每个东欧国家的进口额高于平均每个西亚、北非国家的进口额