题目内容
如图，PT为圆O的切线，T为切点，∠ATM=
，圆O的面积为2π，则PA=______．
| π |
| 3 |
连接OT，由于T是切点，故角OTA=90°，又由∠ATM=
，可求得角TOA=120°，∴∠TOA=60°，∴∠P=30°，
在直角三角形PTO中得PO=2OT=2R，故得PA=3R
又圆的面积是2π，得R=
∴PA=3
故答案为3
| π |
| 3 |
在直角三角形PTO中得PO=2OT=2R，故得PA=3R
又圆的面积是2π，得R=
| 2 |
∴PA=3
| 2 |
故答案为3
| 2 |
练习册系列答案
灵星计算小达人系列答案
相关题目
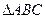的外角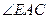
的平分线，交BC的延长线于点D，延长DA交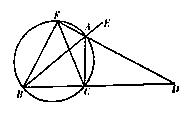
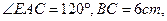求AD的长。
，即每16人抽取一个人.在1～16中随机抽取一个数，如果抽到的是7，则从33～48这16个数中应取的数是（ ）
的学生进行调查，则样本容量和抽取的高中生近视人数分别为（ ）
，
，
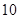
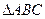中，
//
，
//
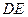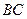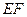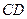，若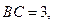
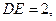
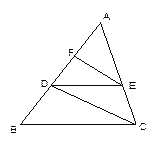
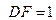，则BD的长为 、AB的长为___________．