题目内容
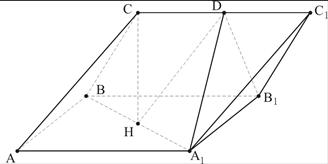
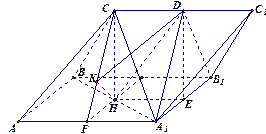
在三棱柱ABC-A1B1C1中,侧 面AA1B1B是边长为2的正方形,点C在平面AA1B1B上的射影H恰好为A1B的中点,且CH=
面AA1B1B是边长为2的正方形,点C在平面AA1B1B上的射影H恰好为A1B的中点,且CH=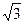 ,设D为
,设D为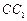 中点,
中点,
(Ⅰ)求证: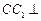 平面
平面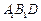 ;
;
(Ⅱ)求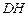 与平面
与平面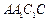 所成角的正弦值.
所成角的正弦值.
 面AA1B1B是边长为2的正方形,点C在平面AA1B1B上的射影H恰好为A1B的中点,且CH=
面AA1B1B是边长为2的正方形,点C在平面AA1B1B上的射影H恰好为A1B的中点,且CH=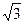 ,设D为
,设D为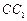 中点,
中点,
(Ⅰ)求证:
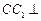 平面
平面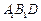 ;
;(Ⅱ)求
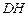 与平面
与平面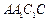 所成角的正弦值.
所成角的正弦值.解:(Ⅰ)因为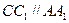
 且正方形中
且正方形中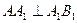 ,所以
,所以
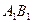 ,
,
取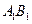 中点
中点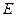 ,则
,则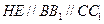 且
且
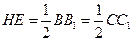 ,又
,又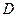 为
为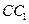 的中点,
的中点,
所以 ,得平行四边形HEDC,
,得平行四边形HEDC,
因此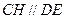 ,又
,又 ,
,
得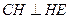 ,
, ,所以
,所以
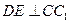
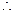
 平面
平面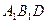 ………………………………6分
………………………………6分
(Ⅱ)取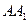 中点
中点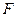 ,连
,连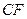 ,作
,作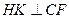 于
于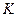
因为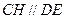 ,
,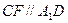 ,所以平面
,所以平面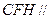 平面
平面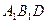 ,由(Ⅰ)得
,由(Ⅰ)得 平面
平面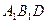 ,
,
所以 平面
平面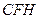 ,又
,又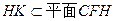 ,所以
,所以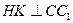 ,又
,又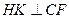 ,得
,得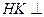 平面
平面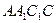 ,所以
,所以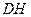 与平面
与平面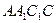 所成角为
所成角为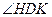 ……………10分
……………10分
在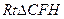 中,
中,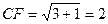 ,
,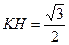
在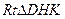 中,由于
中,由于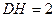 ,
, …………14分
…………14分
另解:(向量法)(Ⅰ)
如图,以H为原点,建立空间直角坐标系,
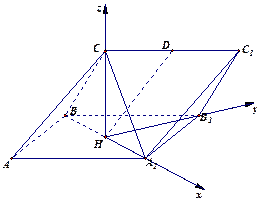
则C(0,0,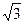 ),C1(
),C1(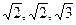 ),A1
),A1
(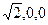 ),B1(0,
),B1(0, ,0),所以
,0),所以
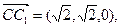

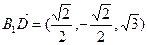
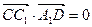 ,
,
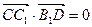 ,因此
,因此 平面
平面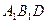 ; ………………6分
; ………………6分
(Ⅱ)设平面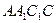 的法向量
的法向量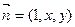 ,由于
,由于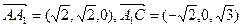
则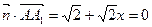 ,
,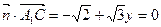
得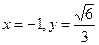 ,所以
,所以 ……………………10分
……………………10分
又 ,所以
,所以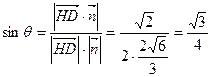 ……14分
……14分
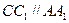
 且正方形中
且正方形中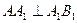 ,所以
,所以
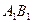 ,
,
取
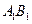 中点
中点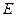 ,则
,则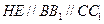 且
且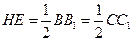 ,又
,又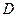 为
为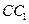 的中点,
的中点,所以
 ,得平行四边形HEDC,
,得平行四边形HEDC,因此
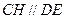 ,又
,又 ,
,得
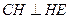 ,
, ,所以
,所以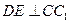
 平面
平面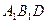 ………………………………6分
………………………………6分(Ⅱ)取
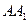 中点
中点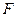 ,连
,连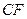 ,作
,作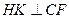 于
于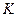
因为
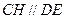 ,
,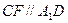 ,所以平面
,所以平面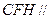 平面
平面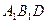 ,由(Ⅰ)得
,由(Ⅰ)得 平面
平面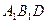 ,
,所以
 平面
平面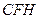 ,又
,又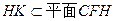 ,所以
,所以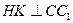 ,又
,又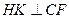 ,得
,得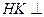 平面
平面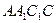 ,所以
,所以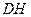 与平面
与平面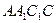 所成角为
所成角为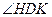 ……………10分
……………10分在
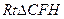 中,
中,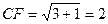 ,
,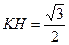
在
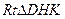 中,由于
中,由于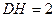 ,
, …………14分
…………14分另解:(向量法)(Ⅰ)
如图,以H为原点,建立空间直角坐标系,

则C(0,0,
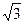 ),C1(
),C1(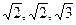 ),A1
),A1(
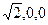 ),B1(0,
),B1(0, ,0),所以
,0),所以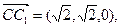

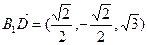
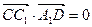 ,
,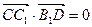 ,因此
,因此 平面
平面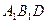 ; ………………6分
; ………………6分(Ⅱ)设平面
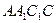 的法向量
的法向量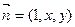 ,由于
,由于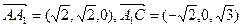
则
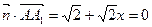 ,
,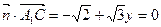
得
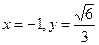 ,所以
,所以 ……………………10分
……………………10分又
 ,所以
,所以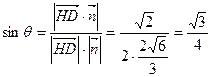 ……14分
……14分略

练习册系列答案
相关题目
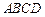 内接于圆柱下底面的圆
内接于圆柱下底面的圆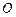 ,
,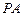 是圆柱的母线,若
是圆柱的母线,若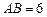 ,
,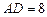 ,此圆柱的体积为
,此圆柱的体积为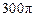 ,求异面直线
,求异面直线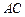 与
与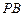 所成角的余弦值.
所成角的余弦值.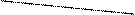
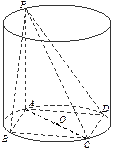

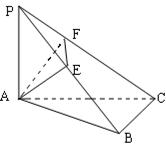
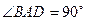 ,AD//BC, AB=
,AD//BC, AB= BC=1,AD=2,PA
BC=1,AD=2,PA 底面ABCD,PD与底面成
底面ABCD,PD与底面成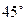 角,点E是PD的中点.
角,点E是PD的中点.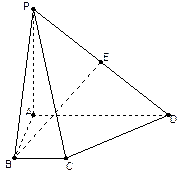
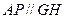
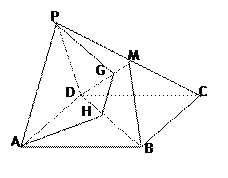
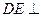 平面ABCD,
平面ABCD,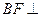 平面ABCD,且FB=2DE=2。
平面ABCD,且FB=2DE=2。
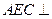 平面AFC。
平面AFC。 ,
,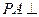 平面
平面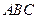 ,
,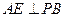 ,
,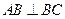 ,
,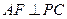 ,
,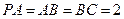 .
.
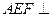 平面
平面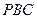 ;
;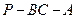 的大小;
的大小;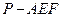 的体
的体 分米,半径是10分米的扇形胶片制作一个圆锥体模型,这个圆锥体的体积等于_ __立方分米.
分米,半径是10分米的扇形胶片制作一个圆锥体模型,这个圆锥体的体积等于_ __立方分米.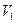 和
和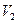 ,则
,则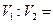 ( )
( )