Question

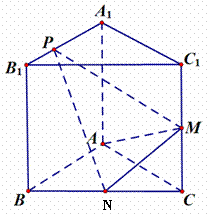
如图，已知三棱柱ABC－A₁B₁C₁的侧棱与底面垂直，AA₁＝AB＝AC＝1，AB⊥AC，M、N分别是CC₁，BC的中点，点P在线段A₁B₁上，且

（1）证明：无论取何值，总有AM⊥PN；

（2）当时，求直线PN与平面ABC所成角的正切值.

 

Answer 1

法一：（1）证明：在三棱柱中，

,而.故

且                               ……………3分

设为的中点、为的中点。连接,.

且,

，

又,,,

故无论取何值，总有                        ……………6分

（2）由于设是

,故

法二  以A为坐标原点，分别以为轴建立空间直角坐标系

则A₁（0，0，1），

B₁（1，0，1）， M（0，1，），N（，0）

，，

C

             ……………4分

N

（1）∵，∴

∴无论取何值，         ……………6分

（2）时，,            ……………8分

而面 设为所成角，

则，                  ……………10分 

所以直线与与平面所成角的正切值为.        ………………12分