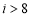题目内容
已知函数 ,且方程
,且方程 有两个实根
有两个实根
(1)求函数 的解析式;
的解析式;
(2)设 ,解关于
,解关于 的不等式
的不等式 .
.
(1) ;(2)当
;(2)当 时,不等式解集为
时,不等式解集为 ;
;
当 时,不等式化为
时,不等式化为 不等式解集为
不等式解集为 ;
;
当 时,不等式解集为
时,不等式解集为 ..
..
【解析】
试题分析:(1)根据题意将两根 分别带入解析式
分别带入解析式 中得到关于
中得到关于 的方程,进而求得
的方程,进而求得 的值,得到
的值,得到 的解析式;(2)利用(1)得到的
的解析式;(2)利用(1)得到的 的解析式,带入
的解析式,带入 进行化简:
进行化简: ,即
,即 ,因为
,因为 ,对
,对 分别分情况进行讨论,进而求得原不等式的解集.
分别分情况进行讨论,进而求得原不等式的解集.
试题解析:(1)分别将 代入方程
代入方程 ,得
,得 解得
解得 所以
所以 (
( ).
).
(2)不等式即为 ,可化为
,可化为 ,即
,即
当 时,不等式解集为
时,不等式解集为 ;
;
当 时,不等式化为
时,不等式化为 不等式解集为
不等式解集为 ;
;
当 时,不等式解集为
时,不等式解集为 .
.
考点:1.待定系数法求函数解析式;2.解分式不等式;3.分类讨论思想.

练习册系列答案
相关题目


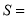 ( )
( )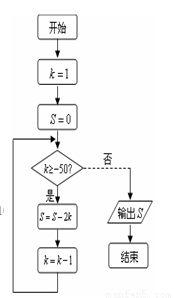
 ,其中
,其中 为正实数,若
为正实数,若 为
为 上的单调函数,则
上的单调函数,则 的取值范围为 .
的取值范围为 . 的焦点为F,过F的直线交该抛物线于A,B两点,则
的焦点为F,过F的直线交该抛物线于A,B两点,则 的最小值为_____________.
的最小值为_____________. 且
且 ,则
,则 从小到大的顺序是___________.
从小到大的顺序是___________. 是定义在
是定义在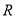 上的偶函数,且
上的偶函数,且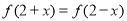 ,当
,当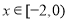 时,
时,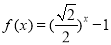 ,若函数
,若函数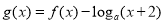
 且
且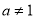 )在区间
)在区间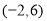 内恰有4个零点,则实数
内恰有4个零点,则实数 的取值范围是( )
的取值范围是( ) B.
B.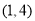 C.
C.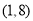 D.
D.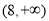
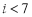 B.
B.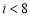 C.
C.  D.
D.