Question

【题目】已知平面向量，，满足：，的夹角为，||＝5，，的夹角为，||＝3，则的最大值为_____．

Answer 1

【答案】36

【解析】

设，，，由题意知四点共圆，建立坐标系，求出点的坐标和圆的半径，设，用表示，根据范围和三角和差公式，即可求解．

设，，，

则AB＝||＝5，AC＝||＝3，∠ACB，∠APB，

可得P，A，B，C四点共圆．

设△ABC的外接圆的圆心为O，则∠AOB＝2∠APB，

由正弦定理可知：2OA5，故OA．

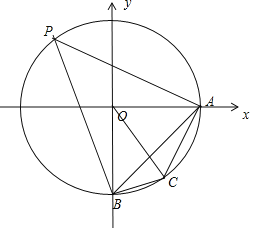
以O为圆心，以OA，OB为坐标轴建立平面坐标系如图所示：

则A（，0），B（0，）．

在△OAC中，由余弦定理可得cos∠AOC，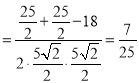

故sin∠AOC，∴C（，）．

设P（cosα，sinα），，

则（cosα，sinα），（cosα，sinα），

∴（cosα）（cosα）sinα（sinα）

＝16+12sinα﹣16cosα＝16+20（sinαcosα）

＝16+20sin（α﹣φ），其中sinφ，cosφ．

∴当α＝φ时，取得最大值36．

答案：36．