题目内容
（2013•延庆县一模）已知|
|=1，|
|=2，向量
与
的夹角为60°，则|
+
|=
．
| a |
| b |
| a |
| b |
| a |
| b |
| 7 |
| 7 |
分析：由条件求得利用两个向量的数量积的定义求得
2、
2、
•
的值，再求得|
+
|2的值，即可得到|
+
| 的值
| a |
| b |
| a |
| b |
. |
| a |
| b |
. |
| a |
| b |
解答：解：∵已知|
|=1，|
|=2，向量
与
的夹角为60°，
∴
2=1，
2=4，
•
=1×2×cos60°=1，．
∴|
+
|2=
2+
2+2
•
=1+4+2=7，
∴|
+
| =
，
故答案为
．
| a |
| b |
| a |
| b |
∴
| a |
| b |
| a |
| b |
∴|
. |
| a |
| b |
| a |
| b |
| a |
| b |
∴|
. |
| a |
| b |
| 7 |
故答案为
| 7 |
点评：本题主要考查两个向量的数量积的定义，求向量的模的方法，属于中档题．
练习册系列答案
相关题目
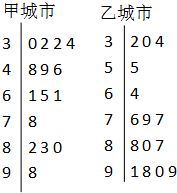（2013•延庆县一模）空气质量指数PM2.5（单位：μg/m3）表示每立方米空气中可入肺颗粒物的含量，这个值越高，就代表空气污染越严重：
（2013•延庆县一模）如图，四棱锥P-ABCD的底面ABCD为菱形，∠ABC=60°，PA⊥底面ABCD，PA=AB=2，E为PA的中点．