题目内容
在直角坐标系xoy中,若角α的始边为x轴的非负半轴,终边为射线 (x≥0).
(x≥0).(1)求
 的值;
的值;(2)若点P,Q分别是角α始边、终边上的动点,且PQ=4,求△POQ面积最大时,点P,Q的坐标.
【答案】分析:(1)由射线l的方程找出斜率即为α的正切值,根据α为第一象限的角,利用同角三角函数间的基本关系求出sinα和cosα的值,然后利用两角和的正弦函数公式及特殊角的三角函数值把所求的式子化简后,把各自的值代入即可求出值;
(2)由P和Q的坐标,利用两点间的基本公式表示出PQ2,把PQ的值代入后,利用基本不等式即可求出ab的最大值,且求出ab取最大值时a与b的值,利用三角形的面积公式,由OP的长与Q点的纵坐标乘积的一半即可表示出三角形POQ的面积,把ab的最大值代入即可求出面积的最大值,然后把求出的a与b代入P和Q的坐标中确定出两点坐标.
解答:解:(1)由射线l的方程为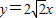 (x≥0),
(x≥0),
得到tanα=2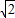 ,且α为第一象限的角,
,且α为第一象限的角,
∴cosα=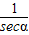 =
=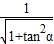 =
= ,
,
则sinα=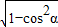 =
=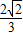 ,
,
故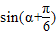 =sinαcos
=sinαcos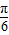 +cosαsin
+cosαsin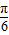 =
=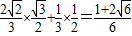 .…4分
.…4分
(2)设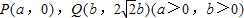 .
.
在△POQ中因为PQ2=(a-b)2+8b2=16,…6分
即16=a2+9b2-2ab≥6ab-2ab=4ab,所以ab≤4 …8分
∴S△POQ= a•3bsinα≤4
a•3bsinα≤4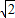 .当且仅当a=3b,即
.当且仅当a=3b,即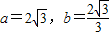 取得等号.…11分
取得等号.…11分
所以△POQ面积最大时,点P,Q的坐标分别为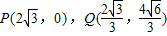 .…15分
.…15分
点评:此题考查了直线倾斜角与斜率之间的关系,同角三角函数间的基本关系,两角和与差的正弦函数公式以及基本不等式,其中根据射线的斜率得到tanα的值是解第一问的突破点.
(2)由P和Q的坐标,利用两点间的基本公式表示出PQ2,把PQ的值代入后,利用基本不等式即可求出ab的最大值,且求出ab取最大值时a与b的值,利用三角形的面积公式,由OP的长与Q点的纵坐标乘积的一半即可表示出三角形POQ的面积,把ab的最大值代入即可求出面积的最大值,然后把求出的a与b代入P和Q的坐标中确定出两点坐标.
解答:解:(1)由射线l的方程为
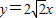 (x≥0),
(x≥0),得到tanα=2
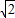 ,且α为第一象限的角,
,且α为第一象限的角,∴cosα=
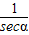 =
=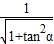 =
= ,
,则sinα=
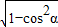 =
=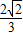 ,
,故
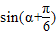 =sinαcos
=sinαcos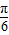 +cosαsin
+cosαsin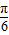 =
=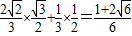 .…4分
.…4分(2)设
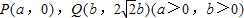 .
.在△POQ中因为PQ2=(a-b)2+8b2=16,…6分
即16=a2+9b2-2ab≥6ab-2ab=4ab,所以ab≤4 …8分
∴S△POQ=
 a•3bsinα≤4
a•3bsinα≤4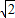 .当且仅当a=3b,即
.当且仅当a=3b,即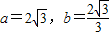 取得等号.…11分
取得等号.…11分所以△POQ面积最大时,点P,Q的坐标分别为
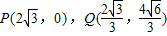 .…15分
.…15分点评:此题考查了直线倾斜角与斜率之间的关系,同角三角函数间的基本关系,两角和与差的正弦函数公式以及基本不等式,其中根据射线的斜率得到tanα的值是解第一问的突破点.

练习册系列答案
相关题目
 如图所示,在直角坐标系xOy中,射线OA在第一象限,且与x轴的正半轴成定角60°,动点P在射线OA上运动,动点Q在y轴的正半轴上运动,△POQ的面积为
如图所示,在直角坐标系xOy中,射线OA在第一象限,且与x轴的正半轴成定角60°,动点P在射线OA上运动,动点Q在y轴的正半轴上运动,△POQ的面积为