题目内容
设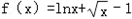 ,证明:
,证明:
(1)当x>1时,f(x)< ( x-1);
( x-1);
(2)当1<x<3时,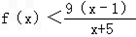 。
。
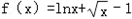 ,证明:
,证明:(1)当x>1时,f(x)<
 ( x-1);
( x-1);(2)当1<x<3时,
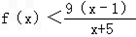 。
。证明:(1)记g(x)=lnx+ -1-
-1- (x-1),
(x-1),
则当x>1时,g′(x)= +
+ -
- <0,
<0,
又g(1)=0,有g(x)<0,即f(x)< ( x-1);
( x-1);
(2)记h(x)=f(x)- ,
,
由(1)得,h′(x)= +
+ -
- =
= -
- <
< -
- =
= ,
,
令g(x)=(x+5)3-216x,
则当1<x<3时,g′(x)=3(x+5)2-216<0,
∴g(x)在(1,3)内是递减函数,
又由g(1)=0,得g(x)<0,
∴h′(x)<0,
因此,h(x)在(1,3)内是递减函数,
又由h(1)=0,得h(x)<0,于是,当1<x<3时,f(x)< 。
。
 -1-
-1- (x-1),
(x-1),则当x>1时,g′(x)=
 +
+ -
- <0,
<0,又g(1)=0,有g(x)<0,即f(x)<
 ( x-1);
( x-1);(2)记h(x)=f(x)-
 ,
,由(1)得,h′(x)=
 +
+ -
- =
= -
- <
< -
- =
= ,
,令g(x)=(x+5)3-216x,
则当1<x<3时,g′(x)=3(x+5)2-216<0,
∴g(x)在(1,3)内是递减函数,
又由g(1)=0,得g(x)<0,
∴h′(x)<0,
因此,h(x)在(1,3)内是递减函数,
又由h(1)=0,得h(x)<0,于是,当1<x<3时,f(x)<
 。
。
练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
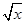 -1,证明:
-1,证明: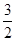 (x-1);
(x-1);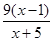 .
.