题目内容
(2013•延庆县一模)在极坐标系下,圆C:ρ2+4ρsinθ+3=0的圆心坐标为( )
分析:先将原极坐标方程化成直角坐标方程,再利用直角坐标方程进行判断.
解答:解:将原方程ρ2+4ρsinθ+3=0化为:
其直角坐标方程为x2+y2+4y+3=0,
它的圆心的直角坐标为(0,-2),
∴圆心的极坐标是:(2,-
).
故选D.
其直角坐标方程为x2+y2+4y+3=0,
它的圆心的直角坐标为(0,-2),
∴圆心的极坐标是:(2,-
| π |
| 2 |
故选D.
点评:本题考查点的极坐标和直角坐标的互化,能在极坐标系中用极坐标刻画点的位置,体会在极坐标系和平面直角坐标系中刻画点的位置的区别,能进行极坐标和直角坐标的互化.利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,等进行代换即得.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
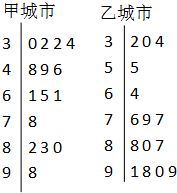 (2013•延庆县一模)空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:
(2013•延庆县一模)空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重: (2013•延庆县一模)如图,四棱锥P-ABCD的底面ABCD为菱形,∠ABC=60°,PA⊥底面ABCD,PA=AB=2,E为PA的中点.
(2013•延庆县一模)如图,四棱锥P-ABCD的底面ABCD为菱形,∠ABC=60°,PA⊥底面ABCD,PA=AB=2,E为PA的中点.