题目内容
已知全集U={R}，集合A={x|log2（3﹣x）≤2}，集合B=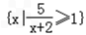 
．
（1）求A、B；
（2）求（CUA）∩B．
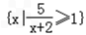．（1）求A、B；
（2）求（CUA）∩B．
解：（1）由已知得：log2（3﹣x）≤log24，
∴
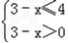解得﹣1≤x＜3，
∴A={x|﹣1≤x＜3}．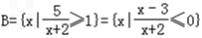
=x|﹣2＜x≤3
∴B={x|﹣2＜x≤3}．
（2）由（I）可得CUA={x|x＜﹣1或x≥3}．
故（CUA）∩B={x|﹣2＜x＜﹣1或x=3}．
∴
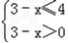解得﹣1≤x＜3，∴A={x|﹣1≤x＜3}．
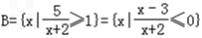=x|﹣2＜x≤3∴B={x|﹣2＜x≤3}．
（2）由（I）可得CUA={x|x＜﹣1或x≥3}．
故（CUA）∩B={x|﹣2＜x＜﹣1或x=3}．
练习册系列答案
相关题目
已知全集U=R，集合A={x|0＜x＞2}，B={x|x＞1}，那么集合A∩(
?UB)=（ ）
| 1 |
| n |
| A、{x|0＜x＜1} |
| B、{x|0＜x≤1} |
| C、{x|1＜x＜2} |
| D、{x|i≤x＜2} |