题目内容
设函数f（x）=（sinωx+cosωx）2+2cos2ωx（ω＞0）的最小正周期为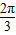
．（Ⅰ）求ω的值；
（Ⅱ）若函数y=g（x）的图象是由y=f（x）的图象向右平移
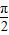个单位长度得到，求y=g（x）的单调增区间．
【答案】分析：（1）先将函数化简为f（x）=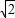
sin（2ωx+
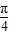），再由
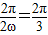，可得答案．
（2）根据g（x）=f（x-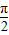
）先求出解析式，再求单调区间．
解答：解：（Ⅰ）f（x）=（sinωx+cosωx）2+2cos2ωx=sin2ωx+cos2ωx+sin2ωx+1+2cos2ωx
=
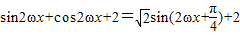
依题意得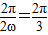
，故ω的值为
．
（Ⅱ）依题意得：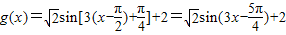
由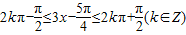
解得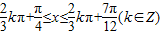
故y=g（x）的单调增区间为：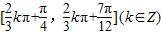
．
点评：本题主要考查三角函数最小正周期的求法和单调区间的求法．做这种题首先要将原函数化简为y=Asin（ωx+φ）的形式再做题．
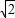sin（2ωx+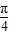），再由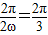，可得答案．（2）根据g（x）=f（x-
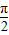）先求出解析式，再求单调区间．解答：解：（Ⅰ）f（x）=（sinωx+cosωx）2+2cos2ωx=sin2ωx+cos2ωx+sin2ωx+1+2cos2ωx
=
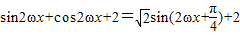
依题意得
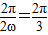，故ω的值为．（Ⅱ）依题意得：
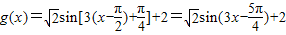
由
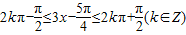
解得
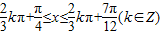
故y=g（x）的单调增区间为：
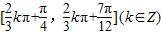．点评：本题主要考查三角函数最小正周期的求法和单调区间的求法．做这种题首先要将原函数化简为y=Asin（ωx+φ）的形式再做题．
练习册系列答案
相关题目