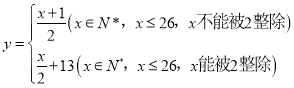题目内容
【题目】已知![]() 位数满足下列条件:①各个数字只能从集合
位数满足下列条件:①各个数字只能从集合![]() 中选取;②若其中有数字
中选取;②若其中有数字![]() ,则在
,则在![]() 的前面不含
的前面不含![]() ,将这样的
,将这样的![]() 位数的个数记为
位数的个数记为![]() ;
;
(1)求![]() 、
、![]() ;
;
(2)探究![]() 与
与![]() 之间的关系,求出数列
之间的关系,求出数列![]() 的通项公式;
的通项公式;
(3)对于每个正整数![]() ,在
,在![]() 与
与![]() 之间插入
之间插入![]() 个
个![]() 得到一个新数列
得到一个新数列![]() ,设
,设![]() 是数列
是数列![]() 的前
的前![]() 项和,试探究
项和,试探究![]() 能否成立,写出你探究得到的结论并给出证明;
能否成立,写出你探究得到的结论并给出证明;
【答案】(1)![]() ,
,![]() (2)
(2)![]() ,
,![]() (3)不能成立,证明见解析
(3)不能成立,证明见解析
【解析】
(1)根据已知条件,进行分类讨论,由此计算出![]() 的值.
的值.
(2)根据已知条件,分类讨论求得![]() 和
和![]() 之间的递推关系式,由此求得数列
之间的递推关系式,由此求得数列![]() 的通项公式.
的通项公式.
(3)根据(2)中求得的数列![]() 的通项公式,计算出
的通项公式,计算出![]() ,由此证得
,由此证得![]() 不成立.
不成立.
(1)当![]() 时,这样的
时,这样的![]() 位数有
位数有![]() 个,所以
个,所以![]() .
.
当![]() 时,若个位数字为
时,若个位数字为![]() ,则十位数字可以为
,则十位数字可以为![]() ,共有
,共有![]() 种;若个位数字为
种;若个位数字为![]() ,则十位数字可以为
,则十位数字可以为![]() ,共有
,共有![]() 种.所以当
种.所以当![]() 时,共有
时,共有![]() 种,即
种,即![]() .
.
当![]() 时,若个位数字是
时,若个位数字是![]() ,则十位和百位的可能情况有
,则十位和百位的可能情况有![]() 种;若个位数字为
种;若个位数字为![]() ,则十位和百位分别有
,则十位和百位分别有![]() 种,共有
种,共有![]() 种.所以
种.所以![]() .
.
(2)结合(1)的分析可知,当![]() 位数时,若个位数字是
位数时,若个位数字是![]() ,其余
,其余![]() 个位置的方法数为
个位置的方法数为![]() ;若个位数字为
;若个位数字为![]() ,则其余
,则其余![]() 个位置的方法数为
个位置的方法数为![]() 种.所以
种.所以![]() .整理得
.整理得![]() ,所以
,所以![]() 是以
是以![]() 为首项,公差为
为首项,公差为![]() 的等差数列,则
的等差数列,则![]() ,化简得
,化简得![]() .所以数列
.所以数列![]() 的通项公式为
的通项公式为![]() .
.
(3)由(2)得![]() .则
.则
![]() ,
,
![]() ,
,
由于![]() ,所以
,所以![]() 单调递增,所以
单调递增,所以![]() 不成立.
不成立.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目