题目内容
【题目】根据国际海洋安全规定：两国军舰正常状况下（联合军演除外），在公海上的安全距离为20
（即距离不得小于20），否则违反了国际海洋安全规定.如图，在某公海区域有两条相交成60°的直航线
，
，交点是
，现有两国的军舰甲，乙分别在
，
上的
，
处，起初
，
，后来军舰甲沿的方向，乙军舰沿
的方向，同时以40
的速度航行.
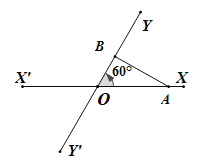
（1）起初两军舰的距离为多少？
（2）试判断这两艘军舰是否会违反国际海洋安全规定？并说明理由.
【答案】（1）
；（2）甲、乙这两艘军舰不会违法国际海洋安全规定，答案见解析.
【解析】
（1）在
中，直接利用余弦定理即可得到
的长；
（2）设
小时后，甲、乙两军舰分别运动到
，
，分
，
两种情况讨论求出CD的长，进一步求得最小值即可.
解：（1）连结，在中，
由余弦定理得
所以：起初两军舰的距离为
.
（2）设小时后，甲、乙两军舰分别运动到，，连结
当时，
当时，
所以经过小时后，甲、乙两军舰距离
因为
因为
，所以当
时，甲、乙两军舰距离最小为
.
又
，所以甲、乙这两艘军舰不会违法国际海洋安全规定.
【点晴】
本题考查余弦定理在解三角形中的应用，考查学生数学运算能力，数学建模能力，是一道中档题.
练习册系列答案
相关题目
