题目内容
已知sin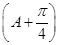 =
=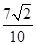 ,A∈
,A∈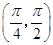 .
.
(1)求cosA的值;
(2)求函数f(x)=cos2x+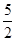 sinAsinx的值域.
sinAsinx的值域.
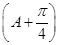 =
=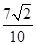 ,A∈
,A∈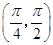 .
.(1)求cosA的值;
(2)求函数f(x)=cos2x+
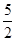 sinAsinx的值域.
sinAsinx的值域.(1) (2)
(2)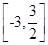
 (2)
(2)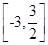
(1)因为 <A<
<A<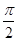 ,且sin
,且sin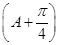 =
=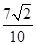 ,所以
,所以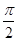 <A+
<A+ <
<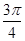 ,cos
,cos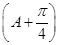 =-
=- .
.
所以cosA=cos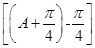 =cos
=cos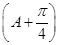 cos
cos +sin
+sin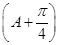 sin
sin =-
=- ·
·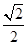 +
+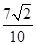 ·
·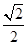 =
= .
.
(2)由(1)可得sinA= .所以f(x)=cos2x+
.所以f(x)=cos2x+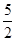 sinAsinx=1-2sin2x+2sinx=-2
sinAsinx=1-2sin2x+2sinx=-2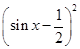 +
+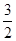 ,x∈R.因为sinx∈[-1,1],所以,当sinx=
,x∈R.因为sinx∈[-1,1],所以,当sinx=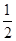 时,f(x)取最大值
时,f(x)取最大值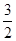 ;当sinx=-1时,f(x)取最小值-3.所以函数f(x)的值域为
;当sinx=-1时,f(x)取最小值-3.所以函数f(x)的值域为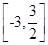
 <A<
<A<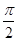 ,且sin
,且sin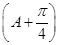 =
=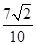 ,所以
,所以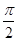 <A+
<A+ <
<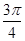 ,cos
,cos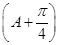 =-
=- .
.所以cosA=cos
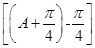 =cos
=cos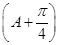 cos
cos +sin
+sin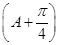 sin
sin =-
=- ·
·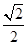 +
+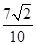 ·
·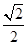 =
= .
.(2)由(1)可得sinA=
 .所以f(x)=cos2x+
.所以f(x)=cos2x+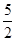 sinAsinx=1-2sin2x+2sinx=-2
sinAsinx=1-2sin2x+2sinx=-2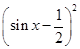 +
+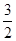 ,x∈R.因为sinx∈[-1,1],所以,当sinx=
,x∈R.因为sinx∈[-1,1],所以,当sinx=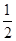 时,f(x)取最大值
时,f(x)取最大值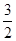 ;当sinx=-1时,f(x)取最小值-3.所以函数f(x)的值域为
;当sinx=-1时,f(x)取最小值-3.所以函数f(x)的值域为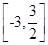

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
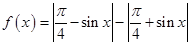 ,则一定在函数
,则一定在函数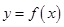 图象上的点是( )
图象上的点是( )



 sin(
sin(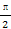 +
+ ,已知函数
,已知函数
 R).
R). 的最小正周期和最大值;
的最小正周期和最大值;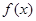 在
在 处取得最大值,且
处取得最大值,且 ,求
,求 的面积
的面积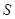 .
. .
. ,且
,且 ,求角
,求角 的值;
的值; ,且
,且 ,求
,求 的值.
的值.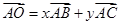 ,且2x+10y=5,则边BC的长
,且2x+10y=5,则边BC的长 是
是 边
边 延长线上一点,记
延长线上一点,记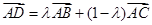 . 若关于
. 若关于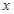 的方程
的方程 在
在 上恰有两解,则实数
上恰有两解,则实数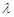 的取值范围是( )
的取值范围是( )
 或
或
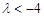 或
或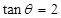 ,则
,则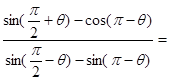 .
.